The theory of the firm and industry equilibrium

Martin J. Osborne
Previous section Previous page Contents Text Exercises Search Next page Next section

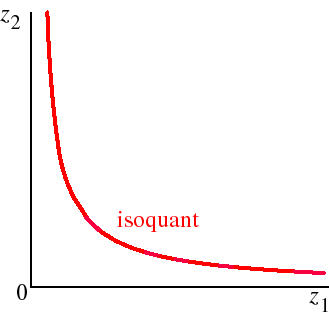
1.3 Isoquants

For a firm that uses two inputs, the set of all pairs (z1, z2) of inputs that yield the output y is the y-isoquant. For the production function F, the y-isoquant is thus the set of all pairs (z1, z2) for which
y = F(z1, z2).

Example: Isoquants for a fixed proportions production function
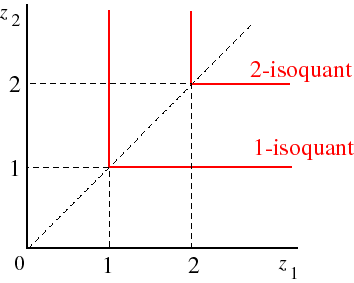
Consider the fixed proportions production function F(z1, z2) = min{z1, z2}. The 1-isoquant is the set of all pairs (z1, z2) for which F(z1, z2) = 1, or min{z1, z2} = 1. That is, the 1-isoquant is the set of all pairs of numbers whose smallest member is 1: the set of all pairs (1, z2) for z2 ≥ 1 and all pairs (z1, 1) for z1 ≥ 1. This set is shown in the following figure, together with the isoquant for output 2.

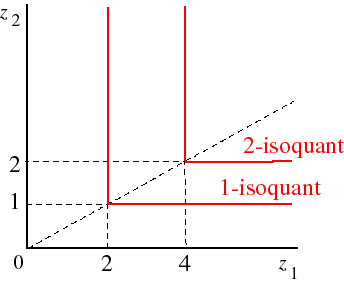
Now consider the fixed proportions production function F(z1, z2) = min{z1/2, z2}, which models a technology in which 2 units of input 1 and 1 unit of input 2 are required to produce every unit of output. The 1-isoquant for this technology is the set of all pairs (z1, z2) for which min{z1/2, z2} = 1. This isoquant, together with the 2-isoquant is shown in the following figure.

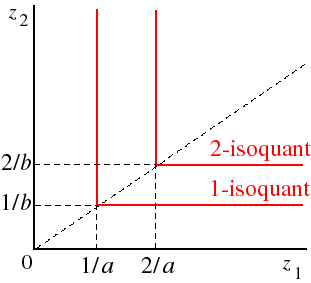
For a general fixed proportions production function F(z1, z2) = min{az1,bz2}, the isoquants take the form shown in the following figure.

Example: Isoquants for a technology in which there are two possible techniques
Consider a technology in which there are two possible techniques. For each technique there is no possibility of substituting one input for another, but various mixes of the two techniques may be used by the firm. For example, perhaps machines can be operated at two possible speeds, fast and slow. If they run fast, then a relatively small amount of labor is used together with a relatively large amount of raw material (since some is wasted). If they run slowly, then a relatively large amount of labor is used together with a relatively small amount of raw material. The firm can run some of its machines fast, and some slowly. An isoquant for such a technology has the form shown in the following figure. (I am considering only raw material and labor as inputs, ignoring the machines.)

The two corners of the isoquant correspond to the cases in which all the machines in the factory run slowly, and in which they all run fast. The points in between, on the downward sloping section, correspond to cases in which the firm runs some of its machines fast and some slowly.

Example: Isoquants for a production function in which the inputs are perfect substitutes
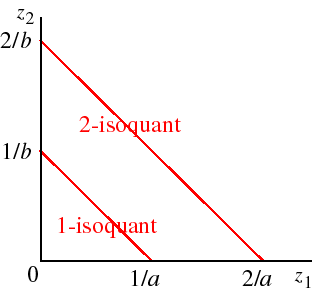
If the production function models a technology in which the inputs are perfect substitutes, then it takes the form
F(z1, z2) = az1 + bz2.
In this case the y-isoquant is the set of all pairs (z1, z2) for which
az1 + bz2 = y,
a straight line with slope −a/b. Thus the isoquants are parallel straight lines:

Example: Isoquants for a Cobb–Douglas production function
Consider the production function
F(z1, z2) = z1/2
1z1/2
2.
The y-isoquant is the set of all pairs (z1, z2) such that
y = z1/2
1z1/2
2,
or
y2 = z1z2.
Thus the y-isoquant is a rectangular hyperbola for every value of y.

For a more general Cobb–Douglas production function the isoquants are not necessarily symmetric about the line z1 = z2, but have the same general shape. For the production function

F(z1, z2) = Azu
1zv
2
the y-isoquant is the set of all pairs (z1, z2) such that
y = Azu
1zv
2.

Marginal rate of technical substitution

The absolute value of the slope of the isoquant through the input pair (z1, z2) is called the marginal rate of technical substitution (MRTS) between input 1 and input 2 at (z1, z2). If, starting at some pair (z1, z2) of inputs, we reduce the value of z1 slightly, then we need to increase the value of z2 to continue producing the same amount of output. The MRTS at (z1, z2) is the ratio of the change in z2 to the change in z1. For example, if the MRTS at (z1, z2) is 2, then if we decrease z1 by a small amount ε then we need to increase z2 by 2ε to continue producing the same amount of output.

MRTS as ratio of MPs

Hold the amount of input 2 fixed at z2 and decrease the amount of input 1 by the small amount Δz1. Then the amount of output decreases by approximately
MP1(z1)Δz1 units,
where MP1 is the marginal product function of input 1 for the fixed amount z2 of input 2.

Now increase the amount of z2 of input 2 by the amount Δz2 in such a way that (z1 − Δz1, z2 + Δz2) is on the same isoquant as (z1, z2). Then the amount of output increases by approximately

MP2(z2)Δz2 units,
where MP2 is the marginal product function of input 2 for the fixed amount z1 − Δz1 of input 1, which, for small values of Δz1, is approximately the same as the marginal product function of input 2 for the fixed amount z1 of input 1.

Along an isoquant output is constant, so the decrease in output caused by the decrease in z1 is equal to the increase caused by the increase in z2. That is,

MP1(z1)Δz1 = MP2(z2)Δz2,
or
Δz2/Δz1 = MP1(z1)/MP2(z2).
The ratio Δz2/Δz1 is the absolute value of the slope of the isoquant, or the MRTS. Thus we conclude that
MRTS(z1, z2) = MP1(z1)/MP2(z2):
the marginal rate of technical substitution is equal to the ratio of the marginal products.
Example: Marginal rate of technical substitution for fixed proportions production function
The isoquants of a production function with fixed proportions are L-shaped, so that the MRTS is either 0 or ∞, depending on the relative magnitude of z1 and z2.

For the specific case

F(z1, z2) = min{z1, z2},
we have
MRTS(z1, z2) = 
left brace ∞  if z1 < z2
0  if z1 > z2
and the MRTS is not defined if z1 = z2. (At points (z1, z2) for which z1 = z2, the isoquants are kinked.)
Example: Marginal rate of technical substitution when inputs are perfect substitutes
The isoquants of a production function for which the inputs are perfect substitutes are straight lines, so the MRTS is constant, equal to the slope of the lines, independent of z1 and z2.

For the specific case

F(z1, z2) = z1 + z2,
the slope of every isoquant is −1, so that
MRTS(z1, z2) = 1
for all values of (z1, z2).

In the general case

F(z1, z2) = az1 + bz2,
the slope of every isoquant is −a/b, so that
MRTS(z1, z2) = a/b
for all values of (z1, z2).
Example: Marginal rate of technical substitution for Cobb–Douglas production function
Consider the production function
F(z1, z2) = z1/2
1z1/2
2.
The y-isoquant of this production function is defined by the condition
y2 = z1z2,
or
z2 = y2/z1.
Differentiating, we obtain
dz2/dz1 = −y2/z2
1 = −z2/z1.
Thus
MRTS(z1, z2) = z2/z1.

In this case the MRTS decreases as more of input 1 is used. We say that a production function with this property has a diminishing marginal rate of technical substitution.