The theory of the firm and industry equilibrium

Martin J. Osborne
Previous section Previous page Contents Text Exercises Search Next page Next section

1.2 Total product, marginal product, and average product

The total product function

Consider a firm with production function F. Suppose that we vary only one input, holding all other inputs fixed. Specifically, assume that there are n inputs and the amount of every input i for i ≠ j is fixed at ki. Then the amount of output the firm can produce as it varies the amount of input j is given by the function Gj defined by
Gj(zj) = F(k1, ..., kj−1, zj, kj+1, ..., kn) for all zj.
For no very good reason, this function is known as a total product function for input j given the values ki for i ≠ j of the other inputs, and is denoted TPj(zj).

Example: fixed proportions
Suppose that there are two inputs and the production technology has fixed proportions, so that the production function takes the form
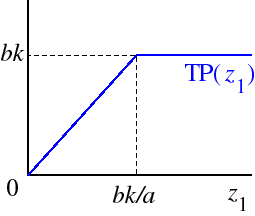
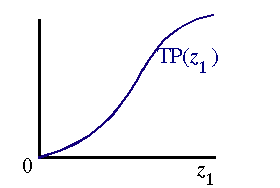
F(z1, z2) = min{az1, bz2},
where a and b are positive constants. If z2 is fixed at k, the total product function for input 1 is
TP1(z1) = min{az1, bk}
or equivalently
TP1(z1) = 
left brace az1  if z1 ≤ bk/a
bk  if z1 > bk/a.
This function is shown in the following figure.

Example: perfect substitutes
If there are two inputs and these inputs are perfect substitutes then the production function takes the form
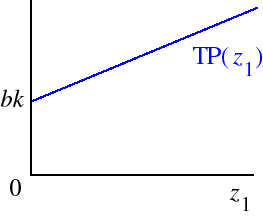
F(z1, z2) = az1 + bz2
where a and b are positive constants. If z2 is fixed at k, the total product function for input 1 is
TP1(z1) = az1 + bk.
This function is shown in the following figure.

Example: Cobb–Douglas production function
If there are two inputs and output is given by a Cobb–Douglas production function then the production function takes the form
F(z1, z2) = Azu
1zv
2,
where A, u, and v are positive constants. If z2 is fixed at k, the total product function for input 1 is
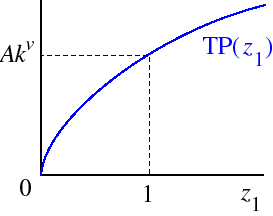
TP1(z1) = Azu
1kv.
For u = 1/2 this function is shown in the following figure.

Now think about a production process that consists of many steps. Fix the amount of machinery, and consider how output may change as the number of workers increases. Conceivably when the number of workers is small, production per worker is relatively small because each worker has to move from one machine to another as an item is produced. As the number of workers increases, output per worker may rise because each worker can dedicate their time to a single process or a small number of processes. But beyond some point, adding more workers has little effect on output—the workers just get in each other's way. If we model the number of workers as a continuous variable, we might get a total product function that looks something like this:

The marginal product and average product functions

A useful concept when thinking about how the output of a firm varies as it changes one input, holding all other inputs fixed, is the rate of increase of the total product, known as the marginal product of the input that can be varied. The marginal product for any value of the variable input is the slope of the total product function at that point. In particular, if the total product function is differentiable, the marginal product is the derivative of the total product function.

The average product of input i given the values ki for i ≠ j of the other inputs is defined to be the average output per unit of input i:

APi(zi) = TPi(zi)/zi.

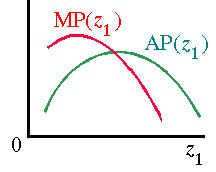
Geometrically, the marginal product for any value of zi is the slope of the total product function at zi; the average product is the slope of a line from the origin to the point (zi, TPi(zi)) on the total product function.

Example: fixed proportions
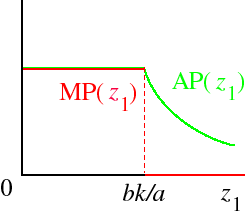
If there are two inputs, the production technology has fixed proportions, and input 2 is fixed at k, the total product function for input 1 is
TP1(z1) =
left brace az1 if z1 ≤ bk/a
bk if z1 > bk/a,
so that the marginal product function of input 1 is
MP1(z1) =
left brace a if z1 ≤ bk/a
0 if z1 > bk/a,
and the average product function of input 1 is
AP1(z1) =
left brace a if z1 ≤ bk/a
bk/z1 if z1 > bk/a.
These functions are illustrated in the following figure.

For example, if F(z1, z2) = min{2z1, 4z2} and the amount z2 of input 2 is fixed at 5, we have TP1(z1) = min{2z1, 20}, or

TP1(z1) =
left brace 2z1 if z1 ≤ 10
20 if z1 > 10,
MP1(z1) =
left brace 2 if z1 ≤ 10
0 if z1 > 10,
and
AP1(z1) =
left brace 2 if z1 ≤ 10
20/z1 if z1 > 10.
Example: perfect substitutes
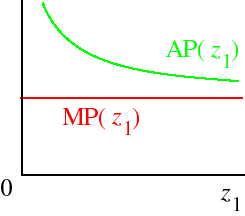
If there are two inputs, the two inputs are perfect substitutes, and input 2 is fixed at k, then the total product function for input 1 is given by
TP1(z1) = az1 + bk
so that the marginal product function of input 1 is
MP1(z1) = a
and the average product function of input 1 is
AP1(z1) = a + bk/z1.
These functions are illustrated in the following figure.

Note that the marginal product is constant, independent of z1: no matter how much of input 1 the firm is using, the extra output it can obtain from one additional unit of the input is the same, equal to a.

Example: Cobb–Douglas production function
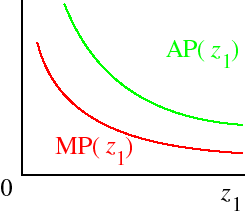
If there are two inputs, the technology is described by a Cobb–Douglas production function, and input 2 is fixed at k, then the total product function for input 1 is given by
TP1(z1) = Azu
1kv
so that the marginal product function of input 1 is
MP1(z1) = Auzu−1
1kv
and the average product function of input 1 is
AP1(z1) = Azu−1
1kv.
These functions are illustrated in the following figure. The values of both functions increase without bound as z1 converges to 0 because u − 1 < 0.

Specifically, if A = 1 and u = v = 1/2, for example,

MP1(z1) = (1/2)z−1/2
1k1/2 = k1/2/(2z1/2
1)
and
AP1(z1) = z−1/2
1k1/2 = k1/2/z1/2
1.

Relation between total, marginal, and average functions in general

Let x be a variable (the amount of an input, the amount of output, ...) and let f(x) be a function of x (total product, total cost, ...). Assume that f is differentiable. The marginal of f is its slope:
M(x) = f'(x).
The average of f is defined by
A(x) = f(x)/x
for x ≠ 0.

A useful relationship between the marginal M and the average A is obtained by differentiating A:

A'(x) = f'(x)/x − f(x)/x2 = [M(x) − A(x)]/x.
Thus
  • if M(x) > A(x) then A is increasing
  • if M(x) = A(x) then A is constant
  • if M(x) < A(x) then A is decreasing.
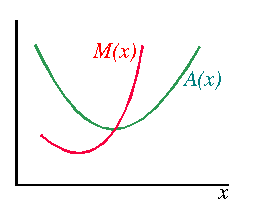
That is: whenever M exceeds A, A is increasing, and whenever M is less than A, A is decreasing. If A is U-shaped for example, we get the picture

while if A has the shape of an inverted U then we get the picture

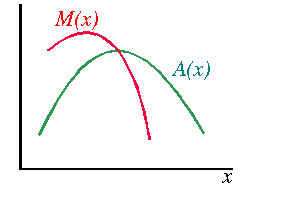
In particular, if the total product function that looks like this

then the average product increases and then decreases, so that the marginal product and average product functions look like this