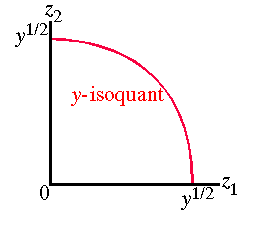The theory of the firm and industry equilibrium

Martin J. Osborne
Previous section Previous page Contents Text Exercises Search Next page Next section

1.3 Exercises on isoquants

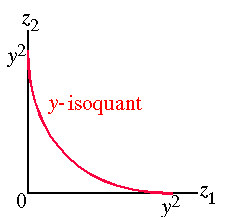
  1. Draw some isoquants for the production function
    F(z1, z2) = z1/2
    1     + z1/2
    2    .

    Solution

    The y-isoquant is given by
    y = z1/2
    1     + z1/2
    2    ,
    or
    z2 = (y − z1/2
    1    )2.
    It is shown in the following figure.

  2. Draw some isoquants for the production function
    F(z1, z2) = z2
    1     + z2
    2    .

    Solution

    The y-isoquant is given by
    y = z2
    1     + z2
    2    .

    It is shown in the following figure.

  3. Find the MRTS for the production function
    F(z1, z2) = z1/2
    1     + z1/2
    2    .

    Solution

    The y-isoquant is given by
    y = z1/2
    1     + z1/2
    2    ,
    or
    z2 = (y − z1/2
    1    )2
    so that
    MRTS(z1, z2) = (y − z1/2
    1    )z−1/2
    1     = (z2/z1)1/2.
    (Remember that the MRTS is the absolute value of the slope of an isoquant.)
  4. Which of the following production functions has a diminishing marginal rate of technical substitution?
    • F(z1, z2) = z1 + z2.
    • F(z1, z2) = z1/2
      1      z1/2
      2      .
    • F(z1, z2) = z2
      1       + z2
      2      .

    Solution

    • For the production function F(z1, z2) = z1 + z2, the isoquants are straight lines. Thus the MRTS is constant, not diminishing.
    • For the production function F(z1, z2) = z1/2
      1      z1/2
      2      , the isoquants are rectangular hyperbolae, hence convex to the origin. Thus the MRTS is diminishing.
    • For the production function F(z1, z2) = z2
      1       + z2
      2      , the isoquants are quarter circles. Thus the MRTS is increasing, not diminishing.