The theory of the firm and industry equilibrium

Martin J. Osborne
Previous section Previous page Contents Text Exercises Search Next page Next section

2.3 The cost function for a firm with two variable inputs

A firm that maximizes its profit must choose the inputs it uses to minimize the cost of producing whatever output it chooses. Its choice of output depends on the environment in which it operates (it may be a monopolist, for example, or may be competing with a few or with many other firms). But whatever the firm's output, the bundle of inputs must be chosen to minimize the cost of producing that output.

Consider a firm that uses two inputs and has the production function F. This firm minimizes its cost of producing any given output y if it chooses the pair (z1, z2) of inputs to solve the problem

minz1,z2w1z1 + w2z2 subject to y = F(z1, z2),
where w1 and w2 are the input prices. Note that w1, w2, and y are given in this problem—they are parameters. The variables are z1 and z2.

Denote the amounts of the two inputs that solve this problem by z*1(y, w1, w2) and z*2(y, w1, w2). The functions z*1 and z*2 are the firm's conditional input demand functions. (They are conditional on the output y, which is taken as given.)

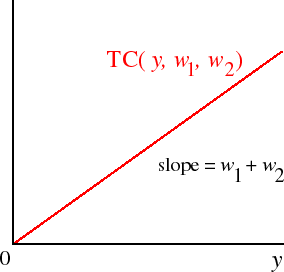
The firm's minimal cost of producing the output y is w1z*1(y,w1, w2) + w2z*2(y,w1, w2) (the value of its total cost for the values of z1 and z2 that minimize that cost). The function TC defined by

TC(y,w1,w2) = w1z*1(y,w1, w2) + w2z*2(y,w1, w2)
is called the firm's (total) cost function.

(Note that the hard part of the problem is finding the conditional input demands; once you have found these, then finding the cost function is simply a matter of adding the conditional input demands together together with the weights w1 and w2.)

Graphical illustration of the cost-minimization problem

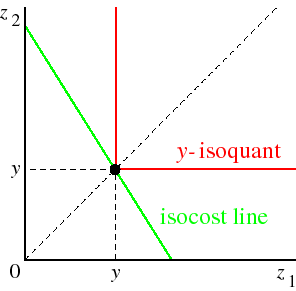
The firm's cost-minimization problem is illustrated in the following figure. The red curve is the y-isoquant: the set of all pairs (z1, z2) of inputs that produce exactly the output y. The light blue area, above the y-isoquant, is the set of all pairs (z1, z2) of inputs that produce at least the output y: the set of feasible input bundles for the output y. Each green line is a set of pairs (z1, z2) of inputs that are equally costly: an isocost line. The points on any given isocost line satisfy the condition
w1z1 + w2z2 = c
for some value of c. Isocost lines further from the origin correspond to higher costs.

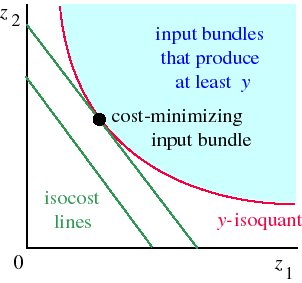
The cost-minimization problem of the firm is to choose an input bundle (z1, z2) feasible for the output y that costs as little as possible. In terms of the figure, a cost-minimizing input bundle is a point on the y-isoquant that is on the lowest possible isocost line. Put differently, a cost-minimizing input bundle must satisfy two conditions:

  • it is on the y-isoquant
  • no other point on the y-isoquant is on a lower isocost line.
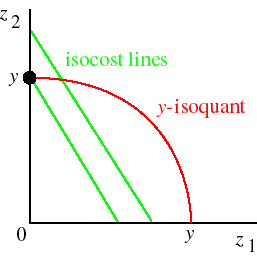
In the figure, there is a single cost-minimizing input bundle, indicated by the black dot.

Another example of a firm's cost-minimization problem is given in the following figure. In this case the isoquant is bowed out from the origin. The cost-minimizing bundle is, as before, the bundle on the isoquant that is on the lowest possible isocost curve. This bundle is indicated by the large black dot. (Note that the point at which an isocost line is tangent to the isoquant maximizes the cost of producing the output y along the isoquant.)

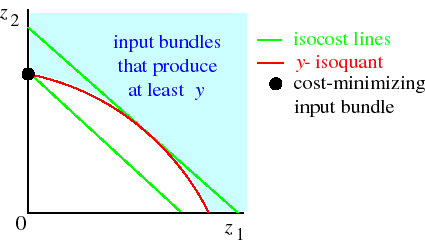
The case of smooth isoquants convex to the origin

If the y-isoquant is smooth and the cost-minimizing bundle involves a positive amount of each input, as in the first figure, we can see that at a cost-minimizing input bundle an isocost line is tangent to the y-isoquant.

Now, the equation of an isocost line is

w1z1 + w2z2 = c
which we can rewrite as
z2 = c/w2 − (w1/w2)z1
so that we see that is slope is −w1/w2. The absolute value of the slope of an isoquant is the MRTS, so we reach the following conclusion.
If the isoquants are smooth and convex to the origin and the cost-minimizing input bundle (z1, z2) involves a positive amount of each input, then this bundle satisfies the following two conditions:
  • (z1, z2) is on the y-isoquant (i.e. F(z1, z2) = y) and
  • the MTRS at (z1, z2) is w1/w2 (i.e. MRTS(z1, z2) = w1/w2).

The condition that the MRTS be equal to w1/w2 can be given the following intuitive interpretation. We know that the MRTS is equal to MP1/MP2. So the condition that the MRTS be equal to w1/w2 is equivalent to the condition

w1/w2 = MP1/MP2,
or
MP1/w1 = MP2/w2:
the marginal product per dollar is equal for the two inputs. That is, the condition that MRTS be equal to w1/w2 is equivalent to the condition that at a cost minimizing bundle, a dollar spent on each input must yield the same marginal output. This condition makes sense: if a dollar spent on input 1 yields more output than a dollar spent on input 2, then more of input 1 should be used and less of input 2. Only if a dollar spent on each input is equally productive is the input bundle optimal.

Example: production function with fixed proportions
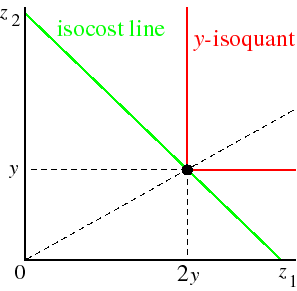
Consider the fixed proportions production function F(z1, z2) = min{z1, z2} (one worker and one machine produce one unit of output). An isoquant and possible isocost line are shown in the following figure.

To produce y units, the firm wants to use y units of each input, no matter what the input prices are. Thus the conditional input demands are

z*1(y,w1,w2) = y and z*2(y,w1,w2) = y.
Hence the total cost function is
TC(y,w1,w2) = w1y + w2y = (w1 + w2)y.
TC is shown as a function of y, for some fixed values of w1 and w2, in the following figure.

Example: production function with fixed proportions
Consider the fixed proportions production function F(z1, z2) = min{z1/2,z2} (two workers and one machine produce one unit of output). An isoquant and possible isocost line are shown in the following figure.

To produce y units, the firm want to use 2y units of input 1 and y units of input 2, no matter what the input prices are. Thus the conditional input demands are

z*1(y,w1,w2) = 2y and z*2(y,w1,w2) = y.
Hence total cost function is
TC(y,w1,w2) = w1·2y + w2y = (2w1 + w2)y.
For fixed values of w1 and w2, this function is linear in y, like the TC function for the previous example.
Example: general production function with fixed proportions
Consider the general fixed proportions production function F(z1, z2) = min{az1, bz2}. To produce y units, the firm wants to use y/a units of input 1 and y/b units of input 2, no matter what the input prices are. Thus the conditional input demands are
z*1(y,w1,w2) = y/a and z*2(y,w1,w2) = y/b.
Hence total cost function is
TC(y,w1,w2) = w1·(y/a) + w2(y/b) = y(w1/a + w2/b).
For fixed values of w1 and w2, this function is linear in y, like the TC function for the previous example.
Example: Cobb–Douglas production function
Consider the production function F(z1, z2) = z1/2
1z1/2
2. The isoquants of this function are smooth and convex to the origin, and for any input prices the firm optimally uses a positive amount of each input. Thus the conditional input demands satisfy the two conditions
y = z1/2
1z1/2
2
and
w1/w2 = MRTS.
The second condition is equivalent to
w1/w2 = z2/z1.
Hence substituting for z2 in the first condition, we find that the conditional input demands satisfy
y = ((w1/w2)z1)1/2·z1/2
1 = (w1/w2))1/2z1.
Isolating z1 and then substituting into the equation w1/w2 = z2/z1 to obtain z2, we conclude that the conditional input demands are
z1 = y(w2/w1)1/2 and z2 = y(w1/w2)1/2.

Thus the total cost function is

TC(y,w1,w2) = w1y(w2/w1)1/2 + w2y(w1/w2)1/2 = 2y(w1w2)1/2.

We see that once again TC is a linear function of output y, given the input prices z1 and z2.

Example: production function in which inputs are perfect substitutes
Consider the production function F(z1, z2) = z1 + z2, in which the inputs are perfect substitutes. An isoquant and some isocost lines for the case in which w1 > w2 are shown in the following figure.

For such input prices, the optimal input bundle is (0,y): the firms uses only input 2. The reason is clear: the inputs may be substituted for one another one-for-one, so if the price of input 1 exceeds the price of input 2 then the firm uses only input 2. Similarly, if w1 < w2 then the firm uses only input 1: the optimal input bundle in this case is (y,0). Finally, if w1 = w2 then the isocost lines have the slope −1, the same as the isoquant. Thus the firm is indifferent about the input bundle it uses.

In summary, the conditional input demands are

z*1(y,w1,w2) =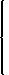 
left brace y if w1 < w2
[0, y] if w1 = w2
0 if w1 > w2

and

z*2(y,w1,w2) =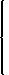 
left brace 0 if w1 < w2
[0, y] if w1 = w2
y if w1 > w2.

Thus the total cost function is

TC(y,w1,w2) =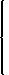 
left brace w1y if w1 < w2
wy if w1 = w2 = w
w2y if w1 > w2.

As in the previous examples, for any fixed values of the input prices the total cost function is linear in output y.

Example: production function with nonconvex isoquants
Suppose that the production function is F(z1, z2) = (z2
1 + z2
2)1/2. In this case the isoquants are quarter-circles. An isoquant and some isocost lines for a case in which w1 > w2 are shown in the following figure.

We see that in this case the optimal input bundle is (0,y). If w1 < w2 then the optimal input bundle is (y,0), and if w1 = w2 then the both (0,y) and (y,0) are optimal, and no other bundles are optimal. Thus the conditional input demands are:

z*1(y,w1,w2) =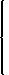 
left brace y if w1 < w2
0 or y if w1 = w2
0 if w1 > w2

and

z*2(y,w1,w2) =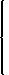 
left brace 0 if w1 < w2
0 or y if w1 = w2
y if w1 > w2.

Thus the total cost function is

TC(y,w1,w2) =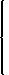 
left brace w1y if w1 < w2
wy if w1 = w2 = w
w2y if w1 > w2.

Once again, for given values of w1 and w2 the cost function is linear in output y.