The theory of the firm and industry equilibrium

Martin J. Osborne
Previous section Previous page Contents Text Search Next page Next section

2.4 Comparative statics for cost-minimizing firm using two inputs

Comparative statics for input prices

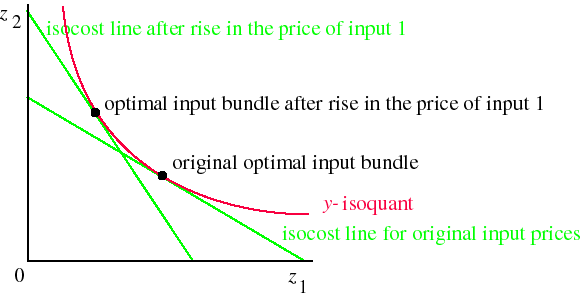
If all input prices change by the same percentage then the price ratio remains the same, so the isocost lines have the same slope, and the optimal input bundle remains the same. Consequently the cost of producing any given output rises by the same percentage as do the input prices.

If one input price increases, while the others remain the same then the slope of the isoquant changes. If the price of input 1 increases, for example, the slope of every isocost line increases. If the isoquant is smooth, the optimal input bundle consequently moves around the isoquant, the amount of input 1 decreasing and the amount of input 2 increasing. The change is shown in the following figure.

More generally, we reach the following conclusion:

Suppose that the cost minimizing quantity of both inputs is positive and that the isoquants are smooth. If the price of input i goes up while the other input prices remain constant, then the cost minimizing quantity of input i decreases and the cost-minimizing quantity of the other input increases.

If the isoquants are not smooth then the optimal input bundle may remain the same as the input price changes. (Think about the case of a fixed proportions production function.)

What happens to the cost of production when one input price increases? In the figure you can see that at the old input prices the new input bundle is more costly than the old bundle: the old isocost line that the new bundle is on is higher than the old isocost line that the old bundle is on. Thus even at the old prices, the new input bundle is more costly than the old input bundle. Since the price of input 1 is higher in the new situation and the price of input 2 is the same, it follows that the new bundle is definitely more costly at the new prices than is the old bundle at the old prices.

The argument may be expressed algebraically. Denote the old input prices (w1, w2) and the old input bundle (z1, z2), and the new prices (w'1, w'2) and the new bundle (z'1, z'2). In the original situation the firm had the option of purchasing the bundle (z'1, z'2), but didn't. Thus (z'1, z'2) must be at least as expensive as (z1, z2) at the old prices:

w1z'1 + w2z'2 ≥ w1z1 + w2z2.
But now w'1 > w1 and w'2 = w2, so that if z'1 > 0 then
w'1z'1 + w'2z'2 > w1z'1 + w2z'2.
We conclude that if z'1 > 0 then
w'1z'1 + w'2z'2 > w1z1 + w2z2,
or
TC(y,w'1, w'2) > TC(y,w1,w2).

In summary:

If the price of an input increases and the firm uses a positive amount of that input to produce some given output then the minimal cost of producing that output increases.

More loosely, if the price of an input increases then the firm substitutes away from it (assuming it continues to produce the same output).

The results are summarized in the following table.

Effect on optimal input bundleEffect on total cost
Every wi rises by x percentStays sameRises by x percent
wi rises, other prices constantLess of input i is usedRises

Comparative statics for level of output

The change in the optimal input bundle when output changes depends on the nature of the production function. The path of all optimal input bundles as output increases is called the output expansion path. The blue line in the following figure is an example of an output expansion path.

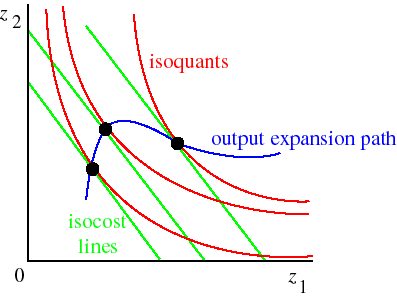
In this example, as output increases initially more of both inputs are used. Then, between the second and third isocost lines the amount of input 2 used starts to decline.

If the optimal amount of an input increases with output then the input is called normal, while if the amount used decreases then the input is called inferior.

Example: a production function with fixed proportions
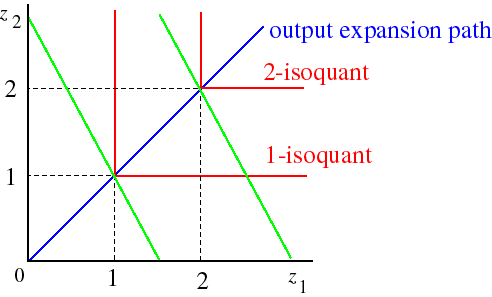
Consider the production function F(z1, z2) = min{z1, z2}. Given the shape of its isoquants, the output expansion path of this production function is a ray from the origin, as in the following figure. For any input prices, the firm uses y units of each input to produce y units of output (see its conditional input demands), so that its output expansion path is the line z2 = z1.

Example: a production function with fixed proportions
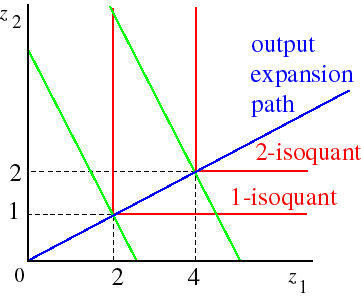
Consider the production function F(z1, z2) = min{z1/2, z2}. Given the shape of its isoquants, the output expansion path of this production function is a ray from the origin, as in the following figure. For any input prices, the firm uses 2y units of input 1 and y units of input 2 to produce y units of output (see its conditional input demands), so that its output expansion path is the line z2 = z1/2.

Example: a general production function with fixed proportions
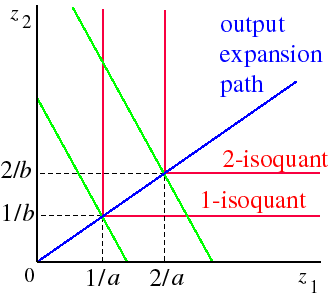
A general production function with fixed proportions takes the form F(z1, z2) = min{az1, bz2} for some constants a and b. Given the shape of its isoquants, the output expansion path of this production function is, as in the previous case, a ray from the origin. For any input prices, the firm uses y/a units of input 1 and y/b units of input 2 to produce y units of output (see its conditional input demands), so that its output expansion path is the line z2 = (a/b)z1.

Example: a production function in which the inputs are perfect substitutes
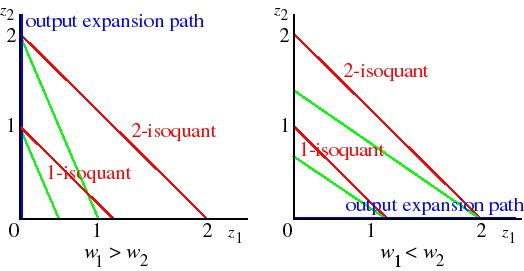
Consider the production function F(z1, z2) = z1 + z2, in which the inputs are perfect substitutes. Given the shape of its isoquants, its output expansion path is
  • the z2 axis if w1 > w2 (if the price of input 1 exceeds that of input 2 then the firm uses none of input 1)
  • the z1 axis if w1 < w2 (if the price of input 2 exceeds that of input 1 then the firm uses none of input 2)
  • the set of all pairs (z1, z2) if w1 = w2 (if the prices of the inputs are the same then every combination of inputs is optimal). [That is, in this case there is not a single output expansion path.]

Example: a general production function in which the inputs are perfect substitutes
The general form of a production function in which the inputs are perfect substitutes is F(z1, z2) = az1 + bz2, for some constants a and b. Given the shape of its isoquants, its output expansion path is
  • the z2 axis (the firm uses none of input 1) if w1 > (a/b)w2
  • the z1 axis (the firm uses none of input 2) if w1 < (a/b)w2
  • the set of all pairs (z1, z2) (every combination of inputs is optimal) if w1 = (a/b)w2. [That is, in this case there is not a single output expansion path.]
Example: a Cobb–Douglas production function
Consider the Cobb–Douglas production function F(z1, z2) = z1/2
1z1/2
2. The conditional input demand functions for this production function are
z1 = y(w2/w1)1/2 and z2 = y(w1/w2)1/2.
Thus the output expansion path satisfies z2/z1 = w1/w2, or
z2 = (w1/w2)z1.
As in all the previous examples, the output expansion path is thus a ray from the origin.

In all these example, the output expansion path a ray from the origin. A production function with this property is called homothetic.