The theory of the firm and industry equilibrium

Martin J. Osborne
Previous section Previous page Contents Text Exercises Search Next page Next section

2.1 The cost function for a firm with one variable input

A firm that can vary only one of its inputs has no choice about the amount of the input it must to produce any given output y. If it uses two inputs to produce output and the amount of input 2 is fixed at k then to produce y units of output it must use the amount z1 of input 1 for which
y = TP(z1,k),
where TP is the total product function.

The cost to the firm of the amount of input 1 necessary to produce y units of output—the variable cost of producing y units of output—is

VC(y) = w1z*1(y),
where z*1(y) is the value of z1 that solves y = TP(z1,k) and w1 is the price of input 1.

The cost of the fixed k units of input 2 is known as the firm's fixed cost and is denoted FC.

The firm's short run total cost, given that the amount of input 2 is fixed at k, is its variable cost plus the cost of the fixed k units of input 2:

STCk(y) = VC(y) + FC = w1z*1 + w2k,
where w2 is the price of input 2. ("STCk" stands for “short run total cost when the amount of the fixed input is k”; we sometimes omit the k subscript when it is clear that the STC is for the case in which the amount of the fixed input is equal to k.)

Average costs and marginal costs

We define the average variable cost, not surprisingly, as the average of the variable cost:
AVC(y) = VC(y)/y
and the average fixed cost as the average of the fixed cost:
AFC(y) = FC/y.
The short run average cost is the average of the short run total cost:
SAC(y) = STC(y)/y = AVC(y) + AFC(y).
The short run marginal cost is the rate of increase of variable cost:
SMC(y) = VC'(y) = STC'(y)
(recall that STC(y) = VC(y) + FC, where FC is independent of output y).

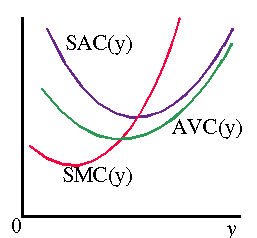
Given the relation between marginals and averages for a general function, if the AVC curve is U-shaped (as we often assume) then the SMC curve is as shown in the figure:

The relation between average product and average cost

Let y be the output produced by z1 units of input 1:
y = TP(z1).
Then we have
AVC(y) = VC(y)/y = w1z1/TP(z1),
or
AVC(y) = w1/[TP(z1)/z1].
But
TP(z1)/z1 = AP(z1),
so that
AVC(y) = w1/AP(z1).
That is, AVC(y) is w1 (a constant) times the reciprocal of AP(z1), where z1 is the amount of input 1 needed to produce y.

The relation between marginal product and marginal cost

Take some amount z1 of input 1 and increase it by Δz1. The resulting increase in cost is
Δc = w1Δz1.
The change in the output is
Δy = MP(z1)Δz1.
Now, short run marginal cost is the rate of change of variable cost: Δc/Δy. So substituting we have
SMC(y) = w1/MP(z1).
That is, SMC(y) is w1 (a constant) times the reciprocal of MP(z1), where z1 is the amount of input 1 needed to produce y.

Example: Fixed proportions
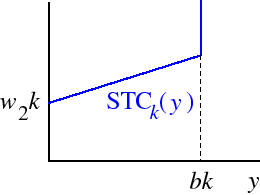
If the firm's production function has fixed proportions then its total product function is
TP(z1) = 
left brace az1 if z1 ≤ bk/a
bk if z1 > bk/a.
Thus it is not possible for the firm to produce more than bk units of output—if you like, its cost of doing so is infinite—and if y ≤ bk then the amount of input 1 needed to produce y units of output is the value of z1 that satisfies
y = az1,
so that
z1 = y/a.
Thus the firm's variable cost of production is
left brace w1y/a if y ≤ bk
∞ if y > bk.
Thus its total cost of production is
STCk(y) = 
left brace w1y/a + w2k if y ≤ bk
bk if y > bk.
This function is shown in the following figure.

Example: Perfect substitutes
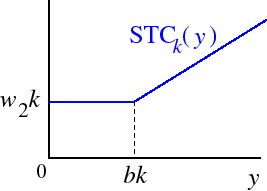
If the firm's production function has perfect substitutes then its total product function is
TP(z1) = az1 + bk.
That is, if it has z1 units of input 1 then the amount of output it produces is
y = az1 + bk.
Thus if it wants to produce at most bk units of output it needs to use no amount of input 1; if it wants to produce more than bk units of output then it needs (y − bk)/a units of z1. That is, the amount of input 1 that it needs is
z1 = 
left brace 0 if y ≤ bk
(y − bk)/a if y > bk.
Thus the firm's variable cost of producing y units of output is
VC(y) = 
left brace 0 if y ≤ bk
w1(y − bk)/a if y > bk,
and its total cost is
STCk(y) = 
left brace w2k if y ≤ bk
w1(y − bk)/a + w2k if y > bk.
This function is shown in the following figure.

Example: Cobb–Douglas production function
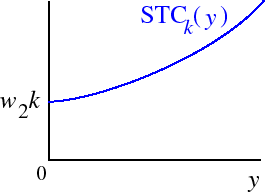
Suppose that firm's production function is
F(z1, z2) = (z1z2)1/2.
(This function is an example of a Cobb–Douglas production function.) Then the firm's total product function is
TP(z1) = z1/2
1k1/2.
Thus the amount of input 1 needed to produce y units of output is the value of z1 that satisfies
y = z1/2
1k1/2.
Isolating z1, we have
z1 = y2/k.
Thus the firm's variable cost of producing y units of output is
VC(y) = w1y2/k
and its total cost is
STCk(y) =w1y2/k + w2k.
This function is shown in the following figure.