The theory of the firm and industry equilibrium

Martin J. Osborne
Previous section Previous page Contents Text Search Next page Next section

7.4 Cournot's oligopoly model and the competitive model

A justification for studying the competitive model, in which each firm takes the price at which it can sell its output as given, is that the market contains a large number of similar firms, so that changes in the output of any one firm have little effect on the price. We can now consider whether this justification is reasonable. Precisely, we can ask if any of the Nash equilibria of Cournot's model converge to a competitive equilibrium as the number of firms increases.

Suppose that the aggregate demand at the price p is D(p), that D is downward-sloping, and that every firm has a (long run) average cost curve that is U-shaped, with efficient scale of production y* and minimum average cost p*. Assume that anyone can operate a firm, so that the number of potential firms is infinite.

In the long run competitive equilibrium of this market the price is p* and the total output of the firms is D(p*). (The number of active firms is D(p*)/y* (assuming this number is an integer).)

I claim that in a Nash equilibrium of Cournot's model the total output Y of the firms satisfies

D(p*) − y* ≤ Y ≤ D(p*).
Thus if the efficient scale of production y* of a single firm is small relative to the total demand D(p*) at the long run equilibrium price p*, then the total output of the firms in a Nash equilibrium is close to the long run competitive equilibrium total output.

To show that the total output of the firms in a Nash equilibrium satisfies the condition above, I show that it is not possible for this total output to lie outside the range. The following figure is useful when making the argument.

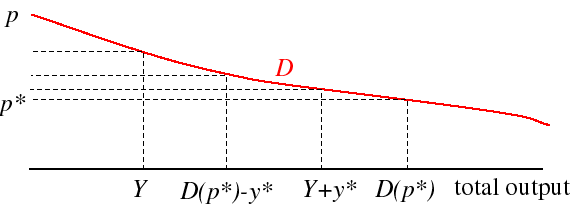
  • If Y > D(p*) then the market price is less than p*, so that every firm makes a loss. Such a situation is not a Nash equilibrium, since any firm can increase its profit to 0 by going out of business.
  • If Y < D(p*) − y* then some firm is inactive (or has an arbitrarily small output). (Remember that there are infinitely many potential firms.) If such a firm deviates and chooses the output y* then the firms' total output becomes Y + y* < D(p*), so that the price still exceeds p*. Hence the deviating firm makes a positive profit, rather than a profit of zero.
(Note that the argument does not imply that there necessarily is a Nash equilibrium---only that if there is one, then it satisfies the stated condition.)

The conclusion is that if the minimum efficient scale y* is small relative to the aggregate demand D(p*) at the competitive price p*, then the total output produced by the firms in a Nash equilibrium is close to the competitive output. More loosely, if firms are small relative to the size of the market then the competitive outcome is close to the Nash equilibrium, so that the assumption of the competitive model that each firm acts as if its actions have no effect on the price is reasonable.

Example
Each of n firms has the cost function TC(y) = 30y; the inverse demand function for the firms' output is p = 120 − Q, where Q is the total output. What are the firms' outputs in a Nash equilibrium of Cournot's model?

The case in which n = 2 is considered in another example. We use the same procedure to find a Nash equilibrium as we did in that case.

  • First find the firms' best response functions. Firm 1's profit is
    y1(120 − y1 − y2 − ... − yn) − 30y1 = y1(120 − y1 − Y1) − 30y1,
    where Y1 = y2 + ... + yn, the total output of all the firms except firm 1. Taking the derivative of this profit with respect to y1 (holding all the other outputs constant) and setting the derivative equal to zero we obtain
    120 − 2y1 − Y1 − 30 = 0,
    or
    y1 = (90 − Y1)/2.
    Thus the best response function of firm 1 is given by
    b1(y2,...,yn) = (90 − Y1)/2.
    The other firms' best response functions are the same, since all the firms' cost functions are the same.
  • We now need to find a list (y1, ..., yn) of outputs with the property that every firm's output is a best response to all the other firms' outputs. Since all the firms are identical, it is reasonable to suppose that there is a Nash equilibrium in which all their outputs are the same: y1 = y2 = ...  = yn. (Note, however, that it does not follow that every Nash equilibrium must take this form.) Denote the common output in this case y*. Then for a Nash equilibrium we need
    y* = b1(y*,...,y*), y* = b2(y*,...y*), ..., y* = bn(y*,...,y*).
    Since all the best response functions are the same, all these equations are the same; we need to solve only one of them. Each one is
    y* = (90 − (n−1)y*)/2,
    or
    y* = 90/(n + 1).
The conclusion is that a Nash equilibrium when there are n firms has each firm producing 90/(n+1) units of output.

In this equilibrium, the total output of the firms is

n(90/(n+1)) = 90n/(n+1)
and the price is
120 − 90n/(n+1).
As n increases, the total output thus approaches 90 and the price approaches 30, the total output and price in the long run competitive equilibrium. That is, if there is a large number of firms then the outcome in a Nash equilibrium of Cournot's model is close to the long run competitive equilibrium.