The theory of the firm and industry equilibrium

Martin J. Osborne
Previous section Previous page Contents Text Search Next page Next section

5.2 Long run competitive equilibrium in an economy with production

Basic theory

In the long run firms can enter and exit the industry.

Theory: A situation is a long run equilibrium if

  • no firm in the industry wants to leave
  • no potential firm wants to enter.

Implications: The theory implies that in a long run equilibrium

  • no existing firm makes a loss
  • any potential firm that entered would make a loss.

Assuming that the technology (and hence cost functions) of every firm are the same, and ignoring the discrete change that may occur in the firms' maximal profits when a firm enters, the theory thus implies that

in a long run equilibrium every firm's maximal profit is zero
or, equivalently,
price is equal to minimum average cost.
Terminology: the output at which LAC is minimal is the efficient scale of production. LAC at the efficient scale of production is thus the minimum average cost. In the following figure, y* is the efficient scale of production and p* is the minimum average cost.

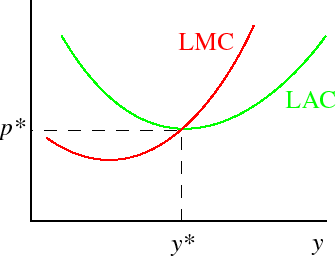
Given this terminology, another implicaton of the theory is:

every firm produces at the efficient scale of production.
What determines the equilibrium number of firms? Given the equilibrium price (minimum average cost), the aggregate demand function Qd gives us the total amount Y* = Qd(p*) that must be produced in equilibrium. We know how much each firm produces in equilibrium (y*, the output equal to its efficient scale of production), so if we divide Y* by this amount we obtain the equilibrium number of firms.

Changes in industry output may affect the cost function

In order to define a long run competitive equilibrium more precisely, we need to take account of the fact that changes in industry output may affect the firms' cost functions.

In the long run, as all firms expand or contract, the change in the industry's demand for inputs may lead to input prices to change. (This is likely to be the case for any input for which the industry uses a significant fraction of the total amount of that input that is available in the economy.) Thus we should index the firms' cost function by industry output: TCY(y) denote the total cost of producing y units of output when the output of the industry is Y. If an increase in industry output leads to an increase in the prices of the inputs used then TC increases in Y: TCY'(y) > TCY(y) for all y whenever Y' > Y. A logical possibility is that TC is decreasing in Y, though this possibility seems unlikely to occur.

Some terminology:

  • if TCY(y) is independent of Y the industry is a constant cost industry.
  • if TCY(y) is increasing in Y for all value of y the industry is an increasing cost industry.
  • if TCY(y) is decreasing in Y for all value of y the industry is an decreasing cost industry.

Definition of a long run competitive equilibrium

Denote by LACY(y) the long run average cost corresponding to TCY(y) (i.e. LACY(y) = TCY(y)/y) and by Qd the aggregate demand function. Then we can define a long run competitive equilibrium precisely as follows.

The long run competitive equilibrium when every firm's long run average cost curve is the same, given by LACY, is characterized by a price p*, an output y* for each firm, and a number n* of firms such that

p* is the minimum of LACn*y*
y* is the minimizer of LACn*y*
Qd(p*) = n*y*.
These conditions are interrelated: the variables p*, y*, and n* appear in each of them. Thus to solve for a long run equilibrium in general we need to solve three simultaneous equations in the three variables p*, y*, and n*.

In the case of a constant cost industry, in which LAC is independent of industry output, the three conditions reduce to

p* is the minimum of LAC
y* is the minimizer of LAC
Qd(p*) = n*y*.
These conditions have a very simple structure: the first one determines p*, the second determines y*, and the last determines n*, given p* and y*. Thus it is straightforward to find the long run equilibrium in a constant cost industry.

Given how the short run and long run cost curves are related, note that in a long run equilibrium we have:

p* = LACY(y*) = SACY,y*(y*) = LMCY(y*) = SMCY,y*(y*),
where SACY,y* and SMCY,y* are the short run cost curves when the aggregate demand is Y = n*y* and the firm's plant is optimal for producing y* units of output.

The long run industry supply function

If the aggregate demand curve shifts (consumers' tastes change, the prices of other goods change, the population increases or decreases, ...) then the long run equilibrium changes. The path of the pairs (Y,p) (where Y is aggregate demand and p is price) traced out as demand changes is called the long run supply function.

Constant cost industry

In a constant cost industry, LAC is independent of industry output, so the long run supply function is horizontal, as in the following figure, which shows the effect of a shift in the aggregate demand curve from D1 to D2. In each case the long run equilibrium price is p* and the output of each firm is y*. When the demand is D1 the number of firms is n1*, and when demand is D2 the number of firms is n2*.

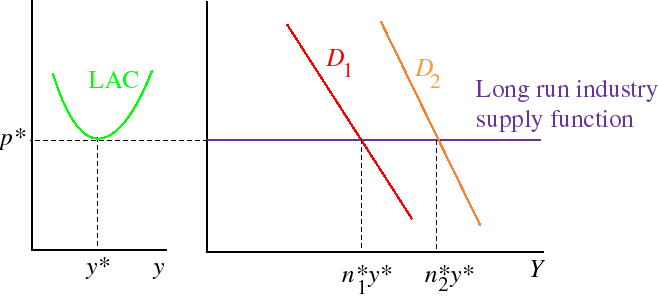
We can tell a dynamic story when the demand shifts. If it shifts to the right, for example,

  • in the short run each firm produces more, and makes profit
  • then more firms enter
  • the short run supply (given the number of firms) therefore moves out
  • the price falls, and each firm reduces its output again.

Increasing cost industry

In an increasing cost industry the cost curve shifts up as industry output increases, so the industry supply curve is upward-sloping. The following figure is drawn under the assumption that as the cost curve shifts up, the efficient scale for each firm remains the same, equal to y*. When the aggregate demand curve is D1 the equilibrium price is p*1 and the number of firms is n*1; when the aggregate demand curve is D2 the equilibrium price is p*2 and the number of firms is n*2.

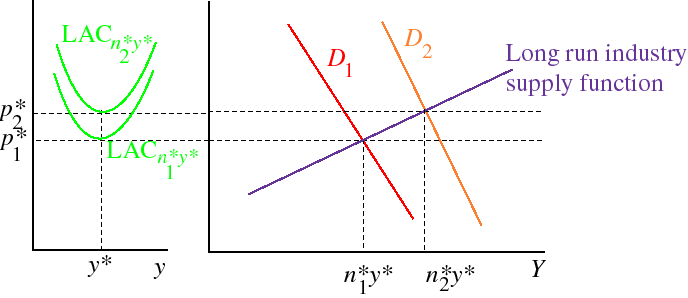
Again we can tell a dynamic story: Initially each of n*1 firms produces y* and the price is p*1. Suppose demand increases from D1 to D2.

  • in the short run price rises, as each firm expands and moves up its short run supply function
  • the profit induces more firms to enter
  • input prices rise as the demand for inputs increases, so LAC rises
  • in the new long run equilibrium there are n*2 firms, each producing y* as before.
Procedure for finding long run competitive equilibrium in constant cost industry
  • Find the minimizer of the LAC, which is the output of each firm in a long run competitive equilibrium.
  • Find the minimum of the LAC, which is the long run equilibrium price.
  • Add together the consumers' demand functions to get the aggregate demand.
  • Divide the the aggregate demand at the equilibrium price by the output of each firm to get the number of firms.
Example
Each firm in an industry has the long run cost function
TC(y) = 
left brace 0 if y = 0
1000 + 10y2 if y > 0.
The aggregate demand function for the output of the firms is Q = 5000−2p. Find the long run equilibrium price, number of firms, and output of each firm.

  • We have LAC(y) = 1000/y + 10y. This is minimized where the derivative is zero: −1000/y2 + 10 = 0, or y = 10. Thus output per firm is 10. [I'm assuming that this is in fact a minimum, not a maximum; it is, since LAC is U-shaped.] [You can alternatively find the minimizer of LAC by equating LAC and LMC: 1000/y + 10y = 20y.]
  • The minimum of LAC is LAC(10) = 200. Thus the long run equilibrium price is 200.
  • Aggregate demand at the price 200 is 5000−400 = 4600, so the number of firms is 4600/10 = 46.
Example
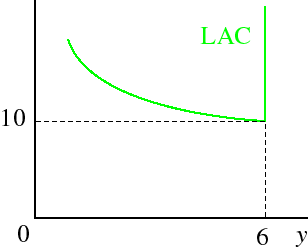
Each firm in an industry has the cost function
TC(y) = 
left brace 0 if y = 0
12 + 8y if 0 < y ≤ 6
∞ if y > 6.
(It has a capacity of 6: it simply cannot produce more than 6 units.) Aggregate demand is given by Qd(p) = 72 − 6p.

Find the long run equilibrium price, output of each firm, and number of firms.

  • We have
    LAC(y) = 
    left brace 12/y + 8 if 0 < y ≤ 6
    ∞ if y > 6.
    This function is shown in the following figure. It is decreasing from 0 to 6, and hence attains a minimum at y = 6. Hence the long run equilibrium output of each firm is 6.

  • The minimum of LAC is LAC(6) = 10. Hence the long run equilibrium price is 10.
  • The aggregate demand at the price 10 is Qd(6) = 36, so the long run equilibrium number of firms is 36/6 = 6.
Example
The total cost function is TC(y) = 2y for each firm. (Note that this implies that the technology has CRTS.) Aggregate demand is Qd(p) = 100 − 4p.

  • LAC(y) = 2, so every output minimizes LAC. Thus the output of each firm is indeterminate. (All outputs are efficient for the firm: the LAC does not have a unique minimum.)
  • The minimum of LAC is 2, so the long run equilibrium price is 2.
  • The aggregate demand at the price 2 is Qd(2) = 92. Since the equilibrium output of each firm is indeterminate, the number of firms is also indeterminate; we know only that the aggregate output of the firms is 92.
Example: the effect of an excise tax
Each firm in an industry has the same U-shaped LAC. The minimum of LAC is $20, which is attained at the output of 50. Aggregate demand is Q = 1000−10p. What is the effect of an excise tax of $10 per unit on the long run equilibrium? How much money does the tax raise?

Before the tax is imposed the equilibrium price is $20 and the equilibrium output of each firm is 50. Total demand at the price $20 is 800, so that there are 16 firms.

The tax raises LAC(y) by 10 for every value of y. Thus the equilibrium price increases to $30 and the output of each firm remains the same. Total demand at the price $30 is 700, so the number of firms decreases to 14.

The amount of money the tax raises is ($10)(700) = $7000.

Example: the effect of an excise tax
Each firm in an industry has LAC(y) = y2 − 200y + 10,100. Aggregate demand is Qd(p) = 4000−10p. Find the long run equilibrium.

  • LAC is minimized where 2y − 200 = 0, or y = 100. Thus the long run equilibrium output of each firm is 100.
  • The minimum of LAC is LAC(100) = (100)2 − 20,000 + 10,100 = 100. Thus the long run equilibrium price is 100.
  • The aggregate demand at the price 100 is Qd(100) = 3000, so there are 3000/100 = 30 firms.

Now suppose a $10 excise tax is imposed on each unit the firm sells. Then, as in the previous example, the firm's LAC rises by $10 at each output, so that the price rises by $10, to $110, the output of each firm stays the same, and demand falls to 2900, so there are 29 firms.

The excise tax therefore raises (29)($10)(100) = $29,000. Each firm pays $1000.

Example: the effect of a lump sum tax
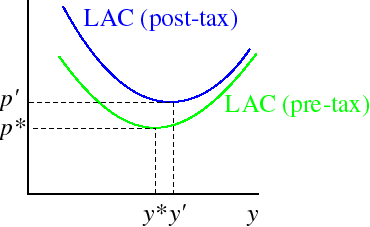
A lump sum tax adds a fixed amount to TC, independent of output. Thus it raises LAC everywhere, but less for larger outputs. Thus the output at which LAC is smallest increases, and the minimal value of LAC increases too. Hence the equilibrium price increases and the output of each firm increases. The change in LAC that the tax causes is shown in the following figure, in which p* and y* are the original equilibrium price and output per firm and p' and y' are the post-tax equilibrium price and output per firm.

Now compare the effect of this lump sum tax with that of an excise tax that raises the equilibrium price by the same amount. Now, an excise tax does not affect output per firm: each firm produces y* after the tax, as it did before the tax. Thus on each unit sold the excise tax yields p' − p*. On the other hand, on each unit sold the lump sum tax raises p' − LAC(y'), which is less than p' − p*. Given that the post-tax price is the same in both cases, so too is the aggregate demand, so that the excise tax raises more revenue than the lump sum tax.

Looking at this result differently, if an excise tax and a lump sum tax raise the same revenue then the lump sum tax must increase price by more than does the excise tax.