The theory of the firm and industry equilibrium

Martin J. Osborne
Previous section Previous page Contents Text Search Next page Next section

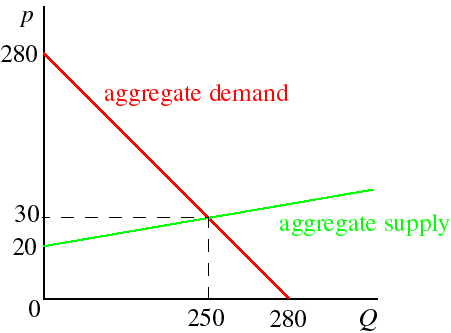
5.1 Short run competitive equilibrium in an economy with production

A short run competitive equilibrium is a situation in which, given the firms in the market, the price is such that that total amount the firms wish to supply is equal to the total amount the consumers wish to demand.

Definition
A short run competitive equilibrium consists of a price p and an output yi for each firm i such that, given the price p, the amount each firm i wishes to supply is yi and the sum ∑iyi of all the firms' outputs is equal to the total amount Qd(p) demanded.

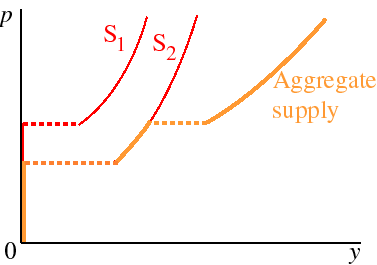
If the firms in the industry have different cost functions, then the aggregate supply function looks something like this:

Now suppose that there are n firms, all with the same cost function, and hence the same short run supply function, say ys. Then a short run competitive equilibrium is a price p and an output y for each firm such that

y = ys(p) and ny = Qd(p).

Pareto stability of short run equilibrium

In an exchange economy in which each individual cares only about the bundle she consumes, the bundle that any other individual consumes, a competitive equilibrium is Pareto stable. Now consider an economy in which goods are produced by firms.

In a competitive equilibrium price is equal to short run marginal cost, so no firm can sell an extra unit at a price that covers its short run marginal cost. Short run marginal cost is the market value of the variable inputs needed to produce the extra unit of output, so in an equilibrium it is not possible to sell another unit at a price that covers the market value of the inputs needed to produce that unit. If the market value of the variable inputs needed to produce an extra unit of output measures their social cost and the price at which a unit can be sold measures the social value of the unit (two big ifs), then in an equilibrium the socially optimal amount of the good is produced.

A rough measure of the consumers' gains from trade is the area under the demand curve and above the price, indicated by the light purple area in the figure below. This area is called the consumers' surplus. A measure of the gain to the producers is the difference between their revenue and their variable cost (since fixed cost is fixed); this measure is called the producers' surplus. The total variable cost is the area under the supply function (which is the marginal cost function) up to the equilibrium output; so the producers' surplus is equal to the area between the supply function and the price, indicated by the pink area in the following figure.

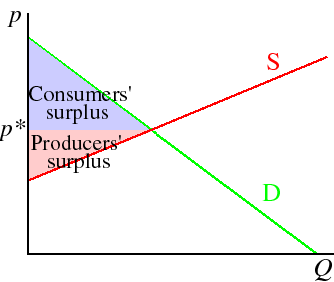
The sum of consumers' surplus and producers' surplus is a measure of the total gains from trade in equilibrium. As you can see, it is maximized in a competitive equilibrium.

Procedure for finding short run competitive equilibrium
  • Find the short run supply function of each firm, which involves
    • finding AVC curve of each firm
    • finding the minimum of the AVC
    • finding the SMC for prices above the minimum AVC.
  • Add together the short run supply functions to get the aggregate short run supply (if there are n identical firms, then we multiply each firm's supply by n).
  • Add together the consumers' demand functions to get the aggregate demand.
  • Equate aggregate demand and aggregate supply to find the equilibrium price.
  • Plug in the equilibrium price to each firm's supply function to find the output of each firm.
Example for finding short run competitive equilibrium
There are 100 consumers, each with the demand function q = 2.2 − p, and 10 firms, each with the fixed cost 10 and variable cost function
VC(y) = 
left brace 2y if y ≤ 5
∞ if y > 5.
(This variable cost function corresponds to a technology with fixed proportions.)

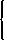
What is a short run competitive equilibrium? What is the total number of units traded, and each firm's profit?

  • The short run supply function for each firm is
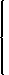
    left brace 0 if p < 2
    all outputs from 0 to 5 if p = 2
    5 if p > 2.
  • Thus the aggregate supply (given that there are 10 firms) is
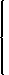
    left brace 0 if p < 2
    all outputs from 0 to 50 if p = 2
    50 if p > 2.
  • The aggregate demand is Qd(p) = 220 − 100p.
  • Since the aggregate demand at the price 2 is 220 − 200 = 20 ≤ 50, the equilibrium price is 2.
  • The output of each firm is indeterminate; each firm produces an output between 0 and 5, such that the total output is the total demand, namely 20.
Each firm's profit is −10 (i.e. each firm makes a loss of 10, equal to its fixed cost). (In the equilibrium, the price is equal to each firm's average variable cost.)
Example for finding short run competitive equilibrium
There are 100 consumers, each with the demand function q = 2.8−0.01p, and 50 firms, each with VC(y) = y2 + 20y and FC(y) = 100.

What is a short run competitive equilibrium? What is the total number of units traded, and each firm's profit?

  • The short run supply function for each firm is
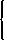
    left brace 0 if p < 20
    (1/2)p − 10 if p ≥ 20.
  • Thus the aggregate supply (given that there are 50 firms) is
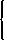
    left brace 0 if p < 20
    25p − 500 if p ≥ 20.
  • The aggregate demand is Qd(p) = 280 − p.
  • The equilibrium price satisfies the equation 25p − 500 = 280 − p if the solution of this equation is at least 20. The solution is p = 30.
  • The output of each firm is (1/2)(30) − 10 = 5.
The supply and demand functions are shown in the following figure.

The total number of units traded is (50)(5) = 250. Each firm's profit is

5·30 − 100 − (20·5 + (5)2) = 150−100−125 = −75.
[NOTE: This loss is less than the fixed cost, as it must be in equilibrium.]
Example for finding short run competitive equilibrium
There are 500 consumers, each with the demand function q = 3.8−0.01p, and 50 firms with cost functions as in the previous example.
  • The short run supply function for each firm is
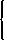
    left brace 0 if p < 20
    (1/2)p − 10 if p ≥ 20.
  • Thus the aggregate supply (given that there are 50 firms) is
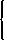
    left brace 0 if p < 20
    25p − 500 if p ≥ 20.
  • The aggregate demand is Qd(p) = 1900 − 5p.
  • The equilibrium price satisfies the equation 25p − 500 = 1900 − 5p if the solution of this equation is at least 20. The solution is p = 80.
  • The output of each firm is (1/2)(80) − 10 = 30.
The total number of units traded is (50)(30) = 1500. Each firm's profit is
30·80 − 100 − (20·30 + (30)2) = 2400 − 100 − 600 − 900 = 800.
That is, each firm makes a profit of $800.
Example for finding short run competitive equilibrium
Modify the previous example by assuming that each firm has to pay an excise tax of $12 per unit, so that VC(y) = y2 + 20y + 12y.
    • AVC(y) = y + 32.
    • The minimum of the AVC is 32, which occurs at y = 0.
    • SMC(y) = 32 + 2y, so the firm's short run supply function is
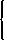
      left brace 0 if p < 32
      (1/2)p − 16 if p ≥ 32.
  • Thus the aggregate supply (given that there are 50 firms) is
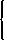
    left brace 0 if p < 32
    25p − 800 if p ≥ 32.
  • The aggregate demand is Qd(p) = 1900 − 5p.
  • The equilibrium price satisfies the equation 25p − 800 = 1900 − 5p if the solution of this equation is at least 32. The solution is p = 90.
  • The output of each firm is (1/2)(90) − 16 = 29.
The total number of units transacted is 1900 − 450 = 1450.

NOTE: The equilibrium price goes up by less ($10) than the amount of the excise tax ($12): the tax burden is shared between the consumers and the producers (since demand is not perfectly inelastic).