6.3 When is a monopoly robust to entry?
To answer the question, we need to model the outcome when there are two firms in the industry. Neither the competitive model nor the monopoly model is appropriate—we really need a model of oligopoly.
But we can do a preliminary analysis if we make the (somewhat unreasonable) assumptions that the monopolist sells its output before another firm enters and does not anticipate entry when choosing its output and, when deciding whether or not to enter, a firm assumes that the monopolist will not react.
Under these assumptions, the question is: given the residual demand—the demand remaining after the monopolist has sold its output—is there any output for an entrant that yields it a positive profit? That is, is there any output for which the residual demand curve lies above the entrant's AC curve?
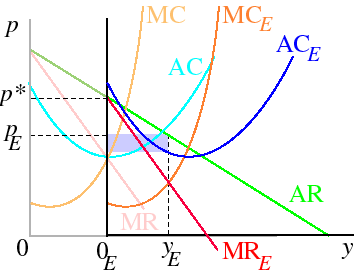
To find the residual demand, we simply subtract the amount sold by the monopolist from the total demand. The model is illustrated in the following figure. The origin for the monopolist is denoted 0. The monopolist produces the output for which MR is equal to MC and charges the price p*. The entrant's origin is 0E, and its marginal cost and average cost curves, relative to this origin, are MCE and ACE. Equating MC with MR, it produces the output yE (measured from the origin 0E) and charges the price pE, and makes a profit equal to the area of the small light purple rectangle.
- Example
-
The demand function for a good is given by Qd(p) = 200 − 2p. The cost function of every potential firm is TC(y) = 20y + F.
If there is a single firm, acting as a profit-maximizing monopolist setting a single price, how much does it produce? What is the price? For what values of F, if any, can another firm that takes the monopolist's output as given make a profit?
We have
TR(y) = y(200−y)/2.SoMR(y) = 100 − y.Further, MC(y) = 20. So the monopolist produces y such that100 − y = 20,ory = 80.The price is p such that80 = 200 − 2por p = 60. The monopolist's profit is(60)(80) − (20)(80) − F = 3200 − F.What demand does an entrant face? The monopolist sells 80 units, so the units remaining for an entrant areQR(p) = 120 − 2p.Thus for an entrant, total revenue isTR(y) = y(120−y)/2.ThusMR(y) = 60 − y.So the entrant produces yE such that60 − yE = 20,oryE = 40.The price it sells at is(120−yE)/2 = 40,so its profit is(40)(40) − (20)(40) − F = 800 − F.Thus the firm is a natural monopoly if F > 800.