The theory of the firm and industry equilibrium

Martin J. Osborne
Previous section Previous page Contents Text Search Next page Next section

2.6 Long run and short run cost functions

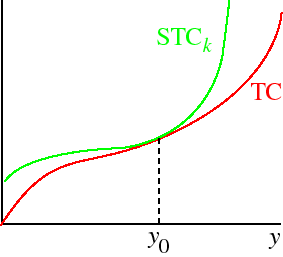
In the long run, the firm can vary all its inputs. In the short run, some of these inputs are fixed. Since the firm is constrained in the short run, and not constrained in the long run, the long run cost TC(y) of producing any given output y is no greater than the short run cost STC(y) of producing that output:
TC(y) ≤ STC(y) for all y.

Now consider the case in which in the short run exactly one of the firm's inputs is fixed. For concreteness, suppose that the firm uses two inputs, and the amount of input 2 is fixed at k. For many (but not all) production functions, there is some level of output, say y0, such that the firm would choose to use k units of input 2 to produce y0, even if it were free to choose any amount it wanted. In such a case, for this level of output the short run total cost when the firm is constrained to use k units of input 2 is equal to the long run total cost: STCk(y0) = TC(y0). We generally assume that for any level at which input 2 is fixed, there is some level of output for which that amount of input 2 is appropriate, so that for any value of k,

TC(y) = STCk(y) for some y.
(There are production functions for which this relation is not true, however: see the example of a production function in which the inputs are perfect substitutes.)

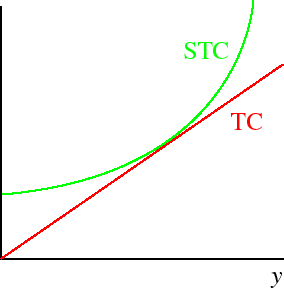
For a total cost function that increases rapidly at first, then less rapidly, and then more rapidly again, the following figure shows the relations between STC and TC.

Example: a production function with fixed proportions
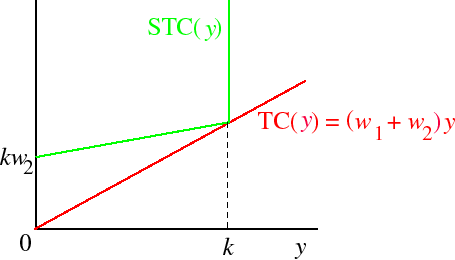
Consider the fixed proportions production function F(z1, z2) = min{z1, z2} (one worker and one machine produce one unit of output). The long run total cost function for this production function is given by
TC(y,w1,w2) = w1y + w2y = (w1 + w2)y.
Its short run total cost of production when the amount of input 2 is fixed at k is
STCk(y) = 
left brace w1y + w2k if y ≤ k
∞ if y > k.
These functions are shown in the following figure.

Example: a production function in which the inputs are perfect substitutes
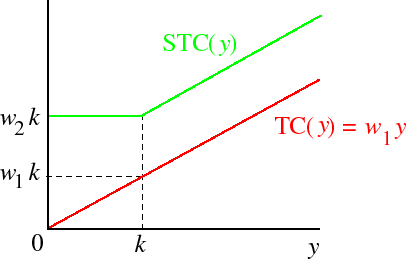
Consider the production function F(z1, z2) = z1 + z2, in which the inputs are perfect substitutes. The long run total cost function for this production function is given by
TC(y,w1,w2) = 
left brace w1y if w1 < w2
wy if w1 = w2 = w
w2y if w1 > w2.
Its short run total cost of production when the amount of input 2 is fixed at k is
STCk(y) = 
left brace w2k if y ≤ k
w1(y − k) + w2k if y > k.
Note that in this case if w1 < w2 then there is no level of output for which short run total cost is equal to the long run total cost. In this case the firm would like to use only input 1 to produce any output, so if k > 0 there is no output for which the short run total cost is equal to the long run total cost. The short and long run cost functions in this case are shown in the following figure.

Example: a Cobb–Douglas production function
Consider the production function F(z1, z2) = z1/2
1z1/2
2. The long run total cost function for this production function is given by
TC(y,w1,w2) = 2y(w1w2)1/2.

Its short run total cost of production when the amount of input 2 is fixed at k is

STCk(y) =w1y2/k + w2k.
Note that TC is a linear function of y while STC is a quadratic function. (Remember that w1 and w2 are fixed.) The functions are shown in the following figure.

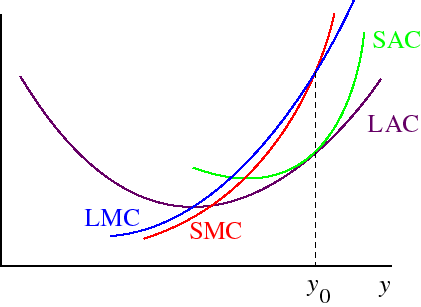
Long run and short run average cost functions

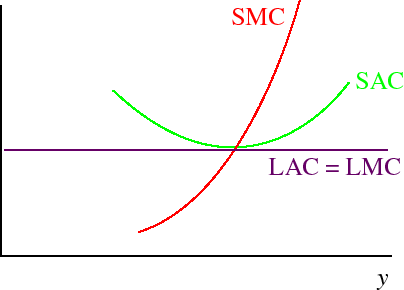
Given the relation between the short and long run total costs, the short and long run average and marginal cost functions have the forms shown in the following figure.

Note:

  • The SMC goes through the minimum of the SAC and the LMC goes through the minimum of the LAC.
  • When SAC = LAC we must have SMC = LMC (since slopes of total cost functions are the same there).
In the case that the production function has CRTS, the LAC is horizontal, as in the following figure.