1.4 Exercises on intervals and functions
- At what points is the function
continuous?
f(x) = 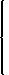
x2 − 2 if x ≤ 0 −x2 if 0 < x < 1 x2 − 2 if x ≥ 1 The function is continuous at all points except 0. We have f(0) = −2, but for x slightly greater than 0, f(x) is close to 0. - Use the Intermediate Value Theorem to show that the equation x7 − 5x5 + x3 − 1 = 0 has a solution between −1 and 1.
Denoting the function by f, we have f(−1) = 2 > 0 and f(1) = −4 < 0. Thus by the Intermediate Value Theorem there exists x between −1 and 1 such that f(x) = 0.