1.4 Intervals and functions
Intervals
- Definition
- An interval is a set of (real) numbers with the property that for every pair of numbers y and z that it contains, it contains also every number between y and z.
- [a, b] = {x: a ≤ x ≤ b} (a and b are included)
- (a, b) = {x: a < x < b} (neither a nor b is included)
- [a, b) = {x: a ≤ x < b} (a is included but b is not)
- (a, b] = {x: a < x ≤ b} (if b is included but a is not).
- (a, ∞) is the interval {x: a < x}.
- (−∞, a] is the interval {x: x ≤ a}.
- (−∞, ∞) is the set of all numbers.
 .
.
In addition to denoting an interval, (a, b) denotes an ordered pair of numbers. The fact that this notation has two meanings is unfortunate. The intended meaning is usually clear from the context; if it is not, complain to the author.
Intuitively, the points a and b are endpoints of the intervals (a, b), (a, b], [a, b), and [a, b], and the remaining points in the intervals are interior to the intervals. Here's how we can precisely distinguish between endpoints and interior points. If x is an endpoint of an interval I, then every interval of the form (x − ε, x + ε), no matter how small ε is as long as it is positive, contains points both in I and outside I. If x is an interior point of an interval I, then we can find a value of ε > 0 such that the interval (x − ε, x + ε) is contained entirely within I. Here are more compact versions of these definitions. Because subsequently we extend the idea of an endpoint to multidimensional sets, we use the more general term “boundary point” in the definition. The distance between two numbers x and y is the absolute value of their difference, |x − y|.
- Definition
-
- A point x is a boundary point of an interval I if for every number ε > 0 (however small), at least one point within the distance ε of x is in I and at least one point within the distance ε of x is outside I.
- A point x is an interior point of an interval I if there is a number ε > 0 such that all points within the distance ε of x are members of I.
- Example 1.4.1
- The set of interior points of the interval [a, b] is (a, b), and the boundary points are a and b.
- Example 1.4.2
- The set of interior points of the interval (a, b) is (a, b), and the boundary points are a and b. Note, in particular, that the boundary points of (a, b) are not members of the set.
- Example 1.4.3
- The set of interior points of the interval (−∞, b) is (−∞, b), and the interval has only one boundary point, b.
- Example 1.4.4
- The set of interior points of the interval (−∞, ∞) is (−∞, ∞), and the interval has no boundary points.
- Definition
-
- The interval I is open if every point in I is an interior point of I.
- The interval I is closed if every boundary point of I is a member of I.
- Example 1.4.5
- The boundary points of the interval [a, b] are a and b, so this interval is closed.
- Example 1.4.6
- The interior of the interval (a, b) is (a, b), the set itself, so this interval is open. The intervals (a, b] and [a, b) are neither open nor closed.
- Example 1.4.7
- The interiors of the intervals (a, b] and [a, b) are both (a, b), so neither interval is open. The boundary points of both intervals are a and b, so neither interval is closed. Thus both intervals are neither open nor closed.
- Example 1.4.8
- The interval consisting of the set of all real numbers, (−∞, ∞), has no boundary points. Thus it is both open and closed.
Sets in n dimensions
We need to consider not only sets of numbers (like intervals), but also sets of n-tuples of numbers. An example of such a set for n = 2 is the set of pairs (“2-tuples”) (x1, x2) such that 0 ≤ x1 ≤ 1 and 0 ≤ x2 ≤ 1, which can be interpreted geometrically as the set of points in a square with side of length 1 and bottom left corner at the origin. Another example, for n = 3, is the set of triples (“3-tuples”) (x1, x2, x3) such thati=1x2
i ≤
- Definition
- An ordered list of n numbers is called an n-vector.
Functions
A function is a rule that associates with every member of some set, a single member of another set. The first set is called the domain of the function. A function with domain A is said to be defined on A.To specify a function we need to specify the domain and the rule. Here are some examples.
- Domain: [−2, 1]. Rule: f(x) = x2.
- Domain: (−∞, ∞). Rule: f(x) = x2.
- Domain: (−1, 1). Rule: f(x) = x if x ≥ 0; f(x) = 1/x if x < 0.
- Domain: union of (0, 1) and (4, 6). Rule: f(x) = √x.
- Domain: set of all pairs of numbers. Rule: f(x, y) = xy.
- Domain: set of n-vectors (x1, ..., xn) for which 0 ≤ xi ≤ 1 for i = 1, ..., n. Rule: f(x1,...,xn) =
∑n
i=1aixi, where a1, ..., an are nonnegative constants.
These examples have two features in common:
- the domain is a subset of the set of n-vectors, for some positive integer n (where n may of course be 1, as in the first four examples)
- the rule associates a real number with each point in the domain.
- Definition
- A function is a rule that associates a number with every point in a set of n-vectors, called the domain of the function. If the domain of a function f is S, we say that f is defined on S. A function whose domain is a set of 1-vectors (i.e. numbers) is called a function of a single variable, and one whose domain is a set of n-vectors for n ≥ 1 as a function of n variables, or, if the specific value of n is not significant, a function of many variables.
The number that a function associates with a given member x of its domain is called the value of the function at x. As x varies over all points in the domain of a function, the value of the function may (and generally does) vary. The set of all such values of the function is called the range of the function.
- Definition
- Let f be a function defined on a set S. The range of f is the set {y: f(x) = y for some x ∈ S}.
- Domain: [−2, 1]. Rule: f(x) = x2. Range: [0, 4].
- Domain: (−∞, ∞). Rule: f(x) = x2. Range: [0, ∞).
- Domain: (−1, 1). Rule: f(x) = x if x ≥ 0; f(x) = 1/x if x < 0. Range: union of (−∞, −1) and [0, 1).
- Domain: union of (0, 1) and (4, 6). Rule: f(x) = √x. Range: union of (0, 1) and (2, √6).
- Domain: set of all pairs of numbers. Rule: f(x, y) = xy. Range: (−∞, ∞).
- Domain: set of n-vectors (x1, ..., xn) for which 0 ≤ xi ≤ 1 for i = 1, ..., n. Rule: f(x1, ..., xn) =
∑n
i=1aixi, where a1, ..., an are nonnegative constants. Range: [0, ∑n
i=1ai].
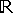 defined by f(x) = √x”, or “for every function f:
defined by f(x) = √x”, or “for every function f: 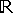 →
→
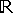 .” (Remember that the symbol
.” (Remember that the symbol 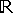 denotes the set of all (real) numbers.) The set B in this notation is called the co-domain or target of the function. Note that this set is not part of the
definition of the function, and may be larger than the range of the function. When we say, for example, “for every function f:
denotes the set of all (real) numbers.) The set B in this notation is called the co-domain or target of the function. Note that this set is not part of the
definition of the function, and may be larger than the range of the function. When we say, for example, “for every function f: 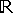 →
→ 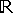 ”, we mean every function whose domain is
”, we mean every function whose domain is
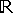 and whose range is a subset of
and whose range is a subset of 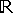 .
.
Graphical illustrations aid the understanding of many functions. A function of a single variable, for example, may be represented on x−y coordinates by plotting, for each value of x, the value of f(x) on the y-axis. An example is shown in the following figure. In this diagram, the small circle indicates a point excluded from the graph: the value of the function at x0 is y0, whereas the value of the function at points slightly greater than x0 is y1.
The red line in this figure is called the graph of the function. Techniques for drawing graphs are discussed in a later section.
Logarithms and exponentials
You need to be comfortable working with the logarithm function and with functions of the form xy (where y is known as an exponent). In particular, you should know the following rules.- xyxz = xy+z
- (xy)z = xyz (so that in particular (xy)1/y = x)
- ln ex = x and eln x = x
- a ln x = ln xa (so that ea ln x = xa).
Continuous functions
A function of a single variable is continuous if its graph has no “jumps”, so that it can be drawn without lifting stylus from tablet (or pen from paper, in an earlier world). More precisely, a function f is continuous at the point a if we can ensure that the value f(x) of the function is as close as we wish to f(a) by choosing x close enough to a. Before giving a completely precise definition for a function of many variables, I give a definition of the (“Euclidean”) distance between two n-vectors, which is the length of the straight line joining them.- Definition
-
The (“Euclidean”) distance between any two n-vectors (x1, ..., xn) and (y1, ..., yn) is
d(x, y) = ∥x − y∥ = √[∑n
i=1(xi − yi)2].
- Definition
- Let f be a function of many variables and let a be a point in its domain. Then f is continuous at a if, for any number ε > 0, there is a number δ > 0 such that for any value of x in the domain of f for which the distance between x and a is less than δ, the difference between f(x) and f(a) is less than ε. A function is continuous if it is continuous at every point in its domain.
The following result is sometimes useful in determining whether a function is continuous.
- Proposition 1.4.1
-
- The sum of continuous functions is continuous: If the functions f and g of many variables are continuous at x0 then the function h defined by h(x) = f(x) + g(x) for all x is continuous at x0.
- The product of continuous functions is continuous: If the functions f and g of many variables are continuous at x0 then the function h defined by h(x) = f(x)g(x) for all x is continuous at x0.
- The quotient of continuous functions is continuous: If the functions f and g of many variables are continuous at x0 and g(x0) ≠ 0 then the function h defined by h(x) = f(x)/g(x) for all x with g(x) ≠ 0 is continuous at x0.
- The composition of continuous functions is continuous: If the function f of many variables is continuous at x0 and the function g of a single variable is continuous at f(x0), then the function h defined by h(x) = g(f(x)) for all x is continuous at x0.
- Proof
-
Denote the distance between the n-vectors x and x' by d(x, x').
Fix ε > 0. In each case we need to show that we can find δ > 0 such that if d(x, x0) < δ then |h(x) − h(x0)| < ε.
For the first part, first note that
The continuity of f at x0 means that we can find δ1 > 0 such that |f(x) − f(x0)| < ε/2 whenever d(x, x0) < δ1, and the continuity of g at x0 means that we can find δ2 > 0 such that |g(x) − g(x0)| < ε/2 whenever d(x, x0) < δ2. Now let δ = min(δ1, δ2). Then if d(x, x0) < δ we have both |f(x) − f(x0)| < ε/2 and |g(x) − g(x0)| < ε/2, so that |f(x) − f(x0)| + |g(x) − g(x0)| < ε, establishing the result.|h(x) − h(x0)| = |(f(x) + g(x)) − (f(x0) + g(x0))| ≤ |f(x) − f(x0)| + |g(x) − g(x0)|. For the second part, we have
The fact that g is continuous at x0 means that we can find δ1 > 0 such that if d(x, x0) < δ1 then |f(x0)||g(x) − g(x0)| < ε/2 and δ2 > 0 such that if d(x, x0) < δ2 then |g(x) − g(x0)| < 1, so that |g(x)| < |g(x0)| + 1. The fact that f is continuous at x0 means that we can find δ3 > 0 such that if d(x, x0) < δ3 then |f(x) − f(x0)| < (ε/2)(1/(|g(x0)| + 1). Now let δ = min(δ1, δ2, δ3). Then if d(x, x0) < δ we have|h(x) − h(x0)| = |g(x)(f(x) − f(x0)) + f(x0)(g(x) − g(x0))| ≤ |g(x)||f(x) − f(x0)| + |f(x0)||g(x) − g(x0)|. establishing the result.|g(x)||f(x) − f(x0)| + |f(x0)||g(x) − g(x0)| < ε, For the third part, I first argue that the function k defined by k(x) = 1/g(x) is continuous at x0. We have
By the continuity of g, there exists δ1 > 0 such that if d(x, x0) < δ1 then |g(x) − g(x0)| < 1, so that 1/|g(x)g(x0)| < 1/(|g(x0) − 1||g(x0)|). Further, for any ε > 0 there exists δ2 > 0 such that if d(x, x0) < δ2 then |g(x) − g(x0)| < ε|g(x0) − 1||g(x0|. Now take δ = min(δ1, δ2). Then if d(x, x0) < δ we have|k(x) − k(x0)| = |1/g(x) − 1/g(x0)| = (1/|g(x)g(x0)|)|g(x0) − g(x)|. establishing that k is continuous at x0. The result then follows from the second part of the proposition.(1/|g(x)g(x0)|)|g(x0) − g(x)| < ε, For the fourth part, the fact that g is continuous at f(x0) means that there exists δ1 > 0 such that if d(f(x), f(x0)) < δ1 then |g(f(x)) − g(f(x0))| < ε. Now, the continuity of f at x0 means that there exists δ2 > 0 such that if d(x, x0) < δ2 then |f(x) − f(x0)| < δ1, and hence |g(f(x)) − g(f(x0))| < ε, establishing the result.
A polynomial is a function of a single variable x of the form a0 + a1x + a2x2 + ... + akxk, where k is a nonnegative integer and a0, ..., ak are any numbers. Because the function f defined by f(x) = x for all x is continuous, the proposition implies that all polynomials are continuous.
The next result gives an important property of continuous functions. It says that if the function f of a single variable on the domain [a, b] is continuous, then f(x) takes on every value from f(a) to f(b).
- Proposition 1.4.2 (Intermediate value theorem)
- If f is a continuous function of a single variable with domain [a,b] and f(a) ≠ f(b), then for any number y between f(a) and f(b), or equal to f(a) or f(b), there is a value of x (in [a,b]) such that f(x) = y.
- Source
- For a proof, see Apostol (1974), Theorem 4.33 on p. 85.
In this figure, the set of values from f(a) to f(b) is shown in red; for every value y in this set, there is a value of x such that f(x) = y. For example, f(x1) = y1. Here are two points to note.
- For some values y between f(a) and f(b) there may be more than one value of x such that y = f(x). For example, in the figure f(x2) = f(x3) = f(x4) = y2.
- The result does not say that for values y greater than f(a) or less than f(b) there is no x such that f(x) = y. Indeed, in the figure we have f(x5) = y3.
An important implication of the result is that if f(a) is positive and f(b) is negative, then f(x) = 0 for some x.
- Example 1.4.9
- Consider the function f defined by f(x) = x4 − 4x2 + 2. Does the equation f(x) = 0 have a solution between 0 and 1? The function is a polynomial, and thus is continuous. We have f(0) = 2 and f(1) = −1, so the Intermediate Value Theorem implies that the answer to the question is yes: for some value of x between 0 and 1 we have f(x) = 0.