Mathematical methods for economic theory

Martin J. Osborne
Previous section Previous page Contents Text Exercises Search Next page Next section

3.4 Exercises on quasiconcavity and quasiconvexity

  1. Draw the upper level sets of each of the following functions for the indicated values. In each case, say whether the set is consistent with the function's being quasiconcave. (Of course, the shape of one upper level set does not determine whether the function is quasiconcave, which is a property of all the upper level sets; the question is only whether the single upper level set you draw is consistent with quasiconcavity.)
    1. f(x, y) = xy for the value 1.
    2. f(x, y) = x2 + y2 for the value 1.
    3. f(x, y) = −x2 − y2 for the value −1.

    Solution

    1. The set is illustrated in red in the following figure. It is not convex (for example, (1, 1) and (−1, −1) are in the set, but (1/2)(1, 1) + (1/2)(−1, −1) = (0, 0) is not), and hence is not consistent with the function's being quasiconcave. (If the domain of the function were restricted to x ≥ 0 and y ≥ 0, then it would be quasiconcave.)

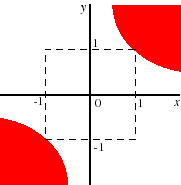
    2. The set is illustrated in red in the following figure. It is not convex (for example, (0, 1) and (0, −1) are in the set, but (1/2)(0, 1) + (1/2)(0, −1) = (0, 0) is not), and hence not consistent with the function's being quasiconcave.

    3. The set is illustrated in red in the following figure. It is convex, and hence consistent with the function's being quasiconcave.

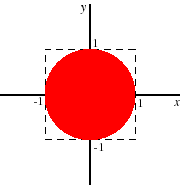
      To show the convexity algebraically, first recall that the triangle inequality says that ∥a + b∥ ≤ ∥a∥ + ∥b∥ for any vectors a and b, where ∥z∥ = (∑n
      i=1      z2
      i      )1/2 for any n-vector z.

      Now let (x, y) and (u, v) be points such that −x2 − y2 ≥ −1 and −u2 − v2 ≥ −1, so that x2 + y2 ≤ 1 and u2 + v2 ≤ 1, or ∥(x, y)∥ ≤ 1 and ∥(u, v)∥ ≤ 1. We need to show that (λx + (1 − λ)u)2 + (λy + (1 − λ)v)2 ≤ 1, or ∥λ(x, y) + (1 − λ)(u, v)∥ ≤ 1.

      By the triangle inequality, for any λ ∈ (0, 1) we have

      ∥λ(x, y) + (1 − λ)(u, v)∥ ≤ ∥λ(x, y)∥ + ∥(1 − λ)(u, v)∥.
      Given that λ ≥ 0 and 1 − λ ≥ 0 we thus have
      ∥λ(x, y) + (1 − λ)(u, v)∥  ≤  λ∥(x, y)∥ + (1 − λ)∥(u, v)∥
       ≤  λ + (1 − λ)
       =  1.
      Hence the set is convex.

  2. For what values of the parameters a, b, c, and d is the function ax3 + bx2 + cx + d quasiconcave? (Use the characterization of quasiconcave functions of a single variable. There are several cases to work through.)

    Solution

    A function f of a single variable is quasiconcave if and only if either it is nondecreasing, or it is nonincreasing, or there is some x* such that f is nondecreasing for x < x* and nonincreasing for x > x*. Consider each case in turn.
    f is nondecreasing
    The derivative of the function is 3ax2 + 2bx + c. In order for this to be nonnegative for all x we certainly need c ≥ 0 (take x = 0). Now, we can consider three cases separately.
    • If a > 0 then the derivative is a convex quadratic, with a minimum at x = −b/3a. (Take the derivative of the derivative, and set it equal to zero.) The minimal value of the derivative is thus 3a·(b/3a)2−2b2/3a + c = −b2/3a + c. For the derivative to be nonnegative for all x it is necessary and sufficient that this minimum be  ≥ 0, which is equivalent to c ≥ b2/3a.
    • If a = 0 then the derivative is nonnegative for all x if and only if b = 0 and c ≥ 0.
    • If a < 0 then the derivative is a concave quadratic, and hence is negative for some values of x, no matter what the values of b and c are.
    f is nonincreasing
    The derivative of the function is 3ax2 + 2bx + c. In order for this to be nonpositive for all x we certainly need c ≤ 0 (take x = 0). Now, as in the previous case, we can consider three cases separately.
    • If a > 0 then the derivative is a convex quadratic, and hence is not nonpositive for all values of x no matter what the values of b and c are.
    • If a = 0 then the derivative is nonpositive for all x if and only if b = 0 and c ≤ 0.
    • If a < 0 then the derivative is a concave quadratic, with a maximum at x = −b/3a. (Take the derivative of the derivative, and set it equal to zero.) The maximal value of the derivative is thus 3a·(b/3a)2−2b2/3a + c = −b2/3a + c. For the derivative to be nonpositive for all x it is necessary and sufficient that this maximum be ≤ 0, which is equivalent to c ≤ b2/3a.
    f increases then decreases
    If a > 0 then the derivative of f is a quadratic; since no quadratic has the property that it is positive up to some point and negative thereafter, the only possibility is that a = 0. In this case f itself is a quadratic; it increases and then decreases if and only if b < 0.

    In summary, f is quasiconcave if and only if either a > 0 and c ≥ b2/3a, or a < 0 and c ≤ b2/3a, or a = 0 and b ≤ 0.

  3. Use the bordered Hessian condition to determine whether the function f(x,y) = ye−x is quasiconcave for the region in which x ≥ 0 and y ≥ 0.

    Solution

    The bordered Hessian of f is
    left parenthesis 0 −ye−x e−x right parenthesis
    −ye−x ye−x −e−x
    e−x −e−x 0
    We have D1(x, y) = −y2e−2x ≤ 0 and D2(x, y) = ye−3x + e−x(ye−2x − ye−2x) = ye−3x ≥ 0. Both determinants are zero if y = 0, so while the bordered Hessian is not inconsistent with the function's being quasiconcave, it does not establish that it is in fact quasiconcave either. However, the test does show that the function is quasiconcave on the domain in which y is restricted to be positive (rather than only nonnegative).

  4. Give an example to show that the sum of quasiconcave functions is not necessarily quasiconcave.

    Solution

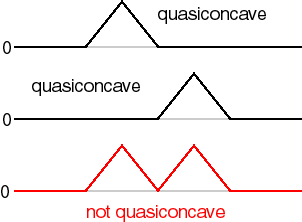
    We can give an example involving functions of a single variable. In the figure, the top and middle functions are quasiconcave (each of them is first nondecreasing, then nonincreasing), whereas the bottom function, which is the sum of the top and middle functions, is not quasiconcave (it is not nondecreasing, is not nonincreasing, and is not nondecreasing then nonincreasing.

  5. The function f is concave and the function g is quasiconcave; neither is necessarily differentiable. Is the function h defined by h(x) = f(x) + g(x) necessarily quasiconcave? (Either show it is, or show it isn't.)

    Solution

    The function h is not necessarily quasiconcave. Suppose, for example, that f and g are functions of a single variable, with f(x) = −x2 and
    g(x) =
    left brace 0 if x < 1
    4x − 4 if x ≥ 1.
    (See the figure below.) Then the function h increases up to x = 0, decreases from x = 0 to x = 1, and then increases up to x = 2, and is thus not quasiconcave.

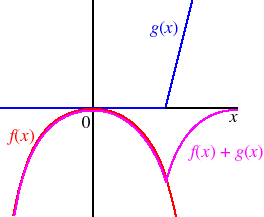
  6. The functions f and g of a single variable are concave (but not necessarily differentiable). Is the function h defined by h(x) = f(x)g(x) necessarily quasiconcave?

    Solution

    No. Let f(x) = x if x ≤ 1 and f(x) = 1 if x > 1, and let g(x) = x if x ≤ 1 and g(x) = 2 − x if x > 1. Then f and g are both concave, but the product, h(x) = x2 if x ≤ 1 and h(x) = 2 − x if x > 1 is not quasiconcave (it decreases, increases, and then decreases).

  7. Determine, if possible, which of the following properties each of the following functions satisfies: convexity, strict convexity, concavity, strict concavity, quasiconcavity, strict quasiconcavity.
    1. f(x,y) = x2y2 for x ≥ 0 and y ≥ 0.
    2. f(x,y) = x − ex − ex+y.

    Solution

    1. The Hessian of the function is
      left parenthesis 2y2 4xy right parenthesis
      4xy 2x2
      The determinant is negative if (x,y) ≠ (0,0), so the function is not concave or convex. To test for quasiconcavity, look at the bordered Hessian:
      left parenthesis 0 2xy2 2x2y right parenthesis
      2xy2 2y2 4xy
      2x2y 4xy 2x2
      We have D1(x,y) = −4x2y4 (the determinant of the 2 × 2 submatrix in the top left). This is zero if (x, y) = (0, 0), so we cannot tell from this test if the function is quasiconcave. (In fact, it is.)
    2. The Hessian of the function is
      left parenthesis −ex−ex+y −ex+y right parenthesis
      −ex+y −ex+y
      Since −ex−ex+y < 0 for all (x, y) and the determinant is (−ex−ex+y)(−ex+y)−(−ex+y)(−ex+y) = e2x+y > 0 for all (x, y) the function is strictly concave, hence strictly quasiconcave. (Or you can argue that since eu is increasing and convex and x + y is convex, ex+y is convex and thus −ex+y is concave, and similarly for −ex; then you need to make a separate argument for strictly concavity.)

  8. The function f of two variables is defined by f(x1, x2) = x1(x2)2. If possible, determine whether this function is quasiconcave for x1 > 0 and x2 > 0. If not possible, say why not.

    Solution

    We have f'1(x1, x2) = (x2)2, f'2(x1, x2) = 2x1x2, f"11(x1, x2) = 0, f"12(x1, x2) = 2x2, and f"22(x1, x2) = 2x1. Thus D1(x1, x2) = −(x2)4 and
    D2(x1, x2) = 
    left parenthesis 0 (x2)2 2x1x2 right parenthesis
    (x2)2 0 2x2
    2x1x2 2x2 2x1
    		,
    so that D2(x1, x2) = 6x1(x2)4. Hence for all (x1, x2) with x1 > 0 and x2 > 0 we have D1(x1, x2) < 0 and D2(x1, x2) > 0, so that f is quasiconcave.

  9. The three curves in the figure below are the sets of points for which the value of the function f (of two variables, x and y) is equal to 1, 2, and 4. Are these curves consistent or inconsistent with the function's being
    1. quasiconcave?

    2. concave?

    Solution

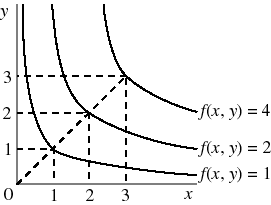
    1. The curves are consistent with the function's being quasiconcave: the sets of points (x, y) such that f(x, y) > a, where 1, 2, and 4, are the sets of points above each curve, and each set is convex. [Note that this fact does not imply that the whole function is necessarily quasiconcave (perhaps some other upper level set is not convex); the question asks you only if the information in the figure is consistent with the function's being quasiconcave.]
    2. The curves are not consistent with the function's being concave: notice that (2, 2) is the midpoint of the line segment from (1, 1) to (3, 3), but the value of the function at (2, 2) is less than the average of the values of the function at (1, 1) and at (3, 3). Stated algebraically, f(2, 2) = 2, while (1/2)f(1, 1) + (1/2)f(3, 3) = (1/2)·1 + (1/2)·4 = (5/2), so that (1/2)f(1, 1) + (1/2)f(3, 3) > f((1/2)(1, 1) + (1/2)(3, 3)) = f(2, 2).

  10. Show that a concave function is quasiconcave by using the fact that a function f is quasiconcave if and only if for all x ∈ S, all y ∈ S, and all λ ∈ [0,1] we have
    if f(x) ≥ f(y) then f((1−λ)x + λy) ≥ f(y).

    Solution

    Take x and y such that f(x) ≥ f(y). By concavity we have f((1−λ)x + λy) ≥ (1−λ)f(x) + λf(y) for all λ with 0 ≤ λ ≤ 1, so that f((1−λ)x + λy) ≥ (1−λ)f(y) + λf(y) = f(y) for all λ with 0 ≤ λ ≤ 1. Thus f is quasiconcave.

  11. Reminder: A function f is quasiconcave if and only if for every x and y and every λ with 0 ≤ λ ≤ 1, if f(x) ≥ f(y) then f((1 − λ)x + λy) ≥ f(y).

    Let U be a function of many variables defined on a convex set S and let g be a function of a single variable defined on a set that contains the range of U. Suppose that U is quasiconcave and g is nondecreasing. Show that the function f defined on S given by f(x) = g(U(x)) is quasiconcave.

    Solution

    Suppose that f(x) ≥ f(y). We need to show that f((1 − λ)x + λy) ≥ f(y) for all λ with 0 ≤ λ ≤ 1. The fact that f(x) ≥ f(y) means that g(U(x)) ≥ g(U(y)), so that, given that g is nondecreasing, U(x) ≥ U(y). Thus U((1 − λ)x + λy) ≥ U(y), because U is quasiconcave, so that, again using the fact that g is nondecreasing, g(U((1 − λ)x + λy)) ≥ g(U(y)), or f((1 − λ)x + λy) ≥ f(y), proving that f is quasiconcave.