Mathematical methods for economic theory

Martin J. Osborne
Previous section Previous page Contents Text Exercises Search Next page Next section

6.3 Exercises on the envelope theorem

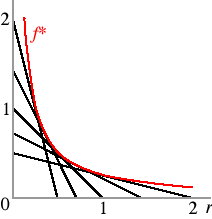
  1. Define the function f by f(x, r) = x1/2 − rx, where x ≥ 0. On a graph with r on the horizontal axis, sketch the function for several values of x. (E.g. sketch the functions (1/2)1/2 − r/2, 11/2 − r, and 21/2 − 2r.) Sketch, in addition, the value function f*, where f*(r) is the maximal value of f(x, r) for each given value of r.

    Solution

    The first-order condition for a solution of the problem of maximizing f is (1/2)x−1/2 = r, so that the solution of the problem for a given value of r is x*(r) = 1/(4r2). Thus f*(r) = 1/4r. The following figure shows the graph of this function, in red, together with the graphs of f(x, r) as a function of r for various values of x.

  2. A firm's output depends upon the amount x of an input and a parameter a, according to the function f(x, a). This function f is increasing in a. The price of the firm's output is p > 0 and the price of the input is w > 0. Determine the sign of the derivative of the firm's maximal profit with respect to a.

    Solution

    Denote the firm's maximal profit by π(a, w, p). By the envelope theorem we have π'1(a, w, p) = pf'2(x, a). Thus since f is increasing in a and p > 0, the derivative of the firm's maximal profit with respect to a is positive.
  3. The output of a good is xay, where x and y are the amounts of two inputs and a > 1 is a parameter. A government-controlled firm is directed to maximize output subject to meeting the constraint 2x + y = 12.
    • Solve the firm's problem.
    • Use the envelope theorem to find how the maximal output changes as the parameter a varies.

    Solution

    The first-order conditions are
    axa−1y − 2λ  =  0
    xa − λ  =  0
    2x + y  =  12
    Solving these we find two solutions: (x*, y*, λ*) = (6a/(1 + a), 12/(1 + a), (6a/(1 + a))a) and (x', y', λ') = (0, 12, 0).

    Since ∇g(x*,y*) ≠ (0,0) the first-order conditions are necessary. That is, if x* solves the problem then it must solve the first-order conditions. By looking at the geometry of the problem, you can convince yourself that indeed the problem has a solution. Since the output from the first solution exceeds the output from the second solution, the solution to the problem is (x*, y*).

    Let M(a) = (x*(a))ay*(a). By the envelope theorem we have

    M'(a)  =  (∂L/∂a)(x*(a), y*(a), a)
     =  (x*(a))ay*(a)ln x*(a)
     =  [12(6a)aln (6a/(1 + a))]/(1 + a)a+1