Mathematical methods for economic theory

Martin J. Osborne
Previous section Previous page Contents Text Exercises Search Next page Next section

3.3 Exercises on concave and convex functions of many variables

  1. By drawing diagrams (or by making precise algebraic arguments), determine which of the following sets is convex.
    1. {(x, y): y = ex}.
    2. {(x, y): y ≥ ex}.
    3. {(x, y): xy ≥ 1, x > 0, y > 0}.

    Solution

    1. Not convex, because eλx+(1−λ)u ≠ λex + (1 − λ)eu, as illustrated in the following figure.

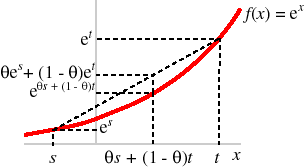
      Specifically, e0 = 1 and e1 = e, but e1/2 ≈ 1.649 and (1/2)1 + (1/2)e ≈ 1.859.

    2. Convex: see the following figure.

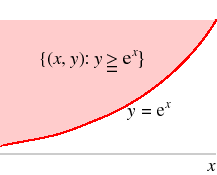
      The function ex is differentiable, and its second derivative is ex > 0, so that it is (strictly) convex. Hence by a result in the text the set of points above its graph, {(x, y): y ≥ ex} is convex.

    3. Convex: see the following figure.

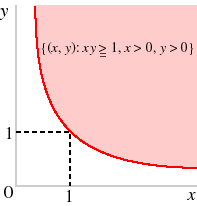
      To show the result algebraically, let xy ≥ 1 and uv ≥ 1. We need to show that (λx + (1 − λ)u)(λy + (1 − λ)v) ≥ 1. We have

      (λx + (1 − λ)u)(λy + (1 − λ)v)  =  λ2xy + λ(1 − λ)(uy + xv) + (1 − λ)2uv.
      Now, uy + xv = uv(y/v) + xy(v/y) ≥ y/v + v/y (given xy ≥ 1 and uv ≥ 1). Also, 0 ≤ (y − v)2 = y2 − 2yv + v2, so y2 + v2 ≥ 2yv, and hence, dividing by yv, y/v + v/y ≥ 2. Thus uy + xv ≥ 2. So, given xy ≥ 1 and uv ≥ 1,
      λ2xy + λ(1 − λ)(uy + xv) + (1 − λ)2uv  ≥  λ2 + 2λ(1 − λ) + (1 − λ)2
       =  (λ + (1 − λ))2
       =  1.

  2. Show that the intersection of two convex sets is convex.

    Solution

    Let A and B be convex sets. Let x ∈ A ⋂ B and x' ∈ A ⋂ B. We need to show that (1 − λ)x + λx' ∈ A ⋂ B for all λ ∈ [0, 1]. Since x ∈ A, x' ∈ A, and A is convex we have (1 − λ)x + λx' ∈ A for all λ ∈ [0, 1]. Similarly (1 − λ)x + λx' ∈ B for all λ ∈ [0, 1]. Hence (1 − λ)x + λx' ∈ A ⋂ B for all λ ∈ [0, 1].

  3. Show that if f and g are concave and a ≥ 0 and b ≥ 0 then the function h defined by h(x) = af(x) + bg(x) for all x is concave.

    Solution

    The fact that f is concave means that for all x, all x', and all λ ∈ (0, 1) we have
    f((1−λ)x + λx')  ≥  (1−λ)f(x) + λf(x')
    and the fact that g is concave means that for all x, all x', and all λ ∈ (0, 1) we have
    g((1−λ)x + λx')  ≥  (1−λ)g(x) + λg(x').
    Thus
    h((1−λ)x + λx')  =  af((1−λ)x + λx') + bg((1−λ)x + λx')
     ≥  a(1−λ)f(x) + aλf(x') + b(1−λ)g(x) + bλg(x')
     =  (1−λ)h(x) + λh(x'),
    so that h is concave.

  4. For each of the following functions, determine which, if any, of the following conditions the function satisfies: concavity, strict concavity, convexity, strict convexity. (Use whatever technique is most appropriate for each case.)
    1. f(x, y) = x + y.
    2. f(x, y) = x2. [Note: f is a function of two variables.]
    3. f(x, y) = x + y − ex − ex+y.
    4. f(x, y, z) = x2 + y2 + 3z2 − xy + 2xz + yz.

    Solution

    1. f((1−λ)x + λx',(1−λ)y + λy') = (1−λ)x + λx' + (1−λ)y + λy' = (1−λ)f(x,y) + λf(x',y'), so the function is concave and convex, but not strictly concave or strictly convex. Or you can calculate the Hessian, from which you can conclude that the function is both concave and convex, and then argue as above that the function is not strictly concave or strictly convex. [Note: the fact that some of the minors are zero does not imply that the function is not strictly concave or strictly convex, although in fact it is not.] Or you can appeal to the fact that the function is linear to conclude that it is concave and convex.
    2. The Hessian shows that the function is convex (all principal minors are nonnegative). The Hessian does not satisfy the sufficient condition for strict convexity, but this does not imply that the function is in fact not strictly convex. However, since, for example, f(1, 1) = f(1, 2) = f(1, 3), the function is in fact not strictly convex. (More generally, for all x, y, and y' we have f((1−λ)(x,y) + λ(x,y')) = f(x,(1−λ)y + λy') = x2 = (1−λ)f(x,y) + λf(x,y').)
    3. The Hessian is
      left parenthesis −ex−ex+y −ex+y right parenthesis
      −ex+y −ex+y
      Since −ex−ex+y < 0 for all (x,y) and the determinant is (−ex−ex+y)(−ex+y)−(−ex+y)(−ex+y) = e2x+y > 0 for all (x,y) the function is strictly concave. (Or you can argue that since eu is increasing and convex and x + y is convex, ex+y is convex and thus −ex+y is concave, and similarly for −ex; then you need to make a separate argument for strict concavity.)
    4. The Hessian is
      left parenthesis 2 −1 2 right parenthesis
      −1 2 1
      2 1 6
      the leading principal minors of which are 2 > 0, 3 > 0, and 4 > 0, so that the function is strictly convex.

  5. The function C of many variables and the function D of a single variable are both convex. Define the function f by f(x,k) = C(x) + D(k). Show that f is a convex function (without assuming that C and D are differentiable).

    Solution

    We have
    f((1−λ)(x,k) + λ(x',k'))  =  C((1−λ)x + λx') + D((1−λ)k + λk')
     ≤  (1−λ)C(x) + λC(x') + (1−λ)D(k) + λD(k')
    by the convexity of C and D. But the right-hand side is (1−λ)f(x,k) + λf(x',k'), showing that f is convex.

  6. The function f (of n variables) is concave, and the function g (of n variables) is convex. Neither function is necessarily differentiable. Is the function h defined by h(x) = af(x) − bg(x), where a ≥ 0 and b ≥ 0 are constants, necessarily concave? (Either show it is, or show it isn't.) Your argument should use only the definition of concavity, and should not refer to any result mentioned in class (or in the book). You won't get any credit for an argument that assumes that f and g are differentiable.

    Solution

    The function f is concave, so
    f((1−λ)x + λy) ≥ (1 − λ)f(x) + λf(y) for all x, y, and λ ∈ (0, 1)
    and the function g is convex, so
    g((1−λ)x + λy) ≤ (1 − λ)g(x) + λg(y) for all x, y, and λ ∈ (0, 1).
    Thus
    h((1−λ)x + λy)  = af((1−λ)x + λy) − bg((1−λ)x + λy)
    ≥ a(1 − λ)f(x) + aλf(y) − b(1 − λ)g(x) − bλg(y).
    Now, the last expression is equal to (1 − λ)(af(x) − bg(x)) + λ(af(y) − bg(y)), which is equal to (1 − λ)h(x) + λh(y), so that h is concave.

  7. The functions f, of many variables, and g, of a single variable, are concave, but not necessarily differentiable. Define the function h by h(x) = g(f(x)) for all x. Is the function h necessarily concave? Necessarily not concave? (Give a complete argument; you will get no credit for an argument that applies only if f and g are differentiable.)

    Solution

    The function h is not necessarily concave: if, for example, f(x) = −x2 and g(z) = −z (which are both concave), then h(x) = x2, which is not concave (it is strictly convex).

    The function h is also not necessarily not concave: if, for example, f(x) = x and g(z) = z (which are both concave), then h(x) = x, which is concave.

  8. Let f(x1, x2) = x2
    1     − x1x2 + x2
    2     + 3x1 − 2x2 + 1. Is f convex, concave, or neither?

    Solution

    The Hessian matrix of f is
    left parenthesis 2 −1 right parenthesis
    −1 2
    		.
    This matrix is positive definite, so f is convex.

  9. Suppose that a firm that uses 2 inputs has the production function f(x1, x2) = 12x1/3
    1    x1/2
    2     and faces the input prices (p1, p2) and the output price 1. Show that f is concave for x1 > 0 and x2 > 0, so that the firm's profit function π, defined by π(x1, x2) = f(x1, x2) − p1x1 − p2x2, is concave. (Show that f is concave from first principles, not from the general result about the concavity of Cobb-Douglas production functions.)

    Solution

    The Hessian matrix at (x1, x2) is
    left parenthesis −(8/3)x−5/3
    1    x1/2
    2    		 2x−2/3
    1    x−1/2
    2    		 right parenthesis
    2x−2/3
    1    x−1/2
    2    		 −3x1/3
    1    x−3/2
    2
    		.
    The leading principal minors are −(8/3)x−5/3
    1    x1/2
    2     < 0 and 8x−4/3
    1    x−1
    2     − 4x−4/3
    1    x−1
    2     = 4x−4/3
    1    x−1
    2     > 0 for x1 > 0 and x2 > 0. Hence the Hessian is negative definite, so that f is concave.

  10. Consider a generalization of this example in which the firm uses a vector x of inputs to produce a single output using the (differentiable) production function f. Denote the vector of input prices by w and the price of the output by p. Suppose that the firm's profit-maximizing input vector for (w, p) is z(w, p) and define the function Π, which gives the firm's maximal profit for any pair (w, p), by
    Π(w, p) = pf(z(w, p)) − wz(w, p).
    Consider two pairs (w', p') and (w", p"). Let x' = z(w', p') and x" = z(w", p"); fix λ ∈ (0, 1) and let x* = z((1 − λ)w' + λw", (1 − λ)p' + λp"). By definition, Π(w', p') ≥ p'f(x) − w'x for all x and Π(w", p") ≥ p"f(x) − w"x for all x. Use these inequalities for x = x* to show that Π is convex.

    Solution

    The inequalities are
    Π(w', p')  ≥ p'f(x*) − w'x*
    Π(w", p")  ≥ p"f(x*) − w"x*.
    Multiply the first inequality by 1 − λ and the second by λ and add them to give
    (1 − λ)Π(w', p') + λΠ(w", p") ≥ (1 − λ)p'f(x*) − (1 − λ)w'x* + λp"f(x*) − λw"x*,
    or
    (1 − λ)Π(w', p') + λΠ(w", p") ≥ ((1 − λ)p' + λp")f(x*) − ((1 − λ)w' + λw")x*,
    or
    (1 − λ)Π(w', p') + λΠ(w", p") ≥ Π((1 − λ)w' + λw", (1 − λ)p' + λp"),
    establishing that Π is convex.

  11. Let f(x1, x2) = x3
    1     + 2x2
    1     + 2x1x2 + (1/2)x2
    2     − 8x1 − 2x2 − 8. Find the range of values of (x1, x2) for which f is convex, if any.

    Solution

    The Hessian matrix of f is
    left parenthesis 6x1 + 4 2 right parenthesis
    2 1
    		.
    This matrix is positive semidefinite if 6x1 + 4 ≥ 0 and 6x1 ≥ 0, or if x1 ≥ 0. Thus f is convex for x1 ≥ 0 (and all x2).

  12. Determine the values of a (if any) for which the function 2x2 + 2xz + 2ayz + 2z2 is concave and the values for which it is convex.

    Solution

    The Hessian of the function is
    left parenthesis 4 0 2 right parenthesis
    0 0 2a
    2 2a 4
    		.
    The first-order minors are 4, 0, and 4, the second-order minors are 0, 12, and −4a2, and the determinant is −16a2. Thus for a = 0 the Hessian is positive semidefinite, so that the function is convex; for other values of a the Hessian is indefinite, so that the function is neither concave nor convex.

  13. Show that the function −w2 + 2wx − x2 − y2 + 4yz − z2 (in the four variables w, x, y, and z) is not concave.

    Solution

    The Hessian is
    left parenthesis −2 2 0 0 right parenthesis
    2 −2 0 0
    0 0 −2 4
    0 0 4 −2
    The second order principal minor obtained by deleting the first and second rows and columns is −12, so the matrix is not negative semidefinite. Thus the function is not concave.