8.6 Second-order differential equations
General form
- Definition
-
A second-order ordinary differential equation is an ordinary differential equation that may be written in the form
x"(t) = F(t, x(t), x'(t))for some function F of three variables.
Equations of the form x"(t) = F(t, x'(t))
An equation of the form- Example 8.6.1
-
Let u be a function of a single variable, with the interpretation that u(w) is the utility of an individual with wealth w. The function ρ defined by
ρ(w) = −wu"(w)/u'(w)is known as the Arrow-Pratt measure of relative risk aversion. (If ρ(w) for the function u exceeds ρ(w) for the function v for all w then u reflects a greater degree of risk-aversion than does v.)
What utility functions have a degree of risk-aversion that is independent of the level of wealth? That is, for what utility functions u do we have
a = −wu"(w)/u'(w) for all wfor some number a?This equation is a second-order differential equation in which the term u(w) does not appear. (The variable is w, rather than t.) Define z(w) = u'(w). Then we have
a = −wz'(w)/z(w)orz'(w)/z(w) = −a/w,a separable first-order ordinary differential equation. Integrating both sides yields∫w(z'(r)/z(r))dr = −a∫w(1/r)dr + C.Making the substitution y = z(r), so that dy = z'(r)dr, we get∫z(w)(1/y)dy = −a∫w(1/r)dr + C,so thatln z(w) = −aln w + Corz(w) = Cw−a.Now, z(w) = u'(w), so to get u we need to integrate:We conclude that a utility function with a constant degree of relative risk-aversion equal to a takes this form.u(w) = 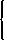
Cln w + B if a = 1 Cw1−a/(1 − a) + B if a ≠ 1.
Linear second-order equations with constant coefficients
- Definition
-
A linear second-order ordinary differential equation with constant coefficients is a second-order ordinary differential equation that may be written in the form
x"(t) + ax'(t) + bx(t) = f(t)for a function f of a single variable and numbers a and b. The equation is homogeneous if f(t) = 0 for all t.
- Proposition 8.6.1
-
Let x be a solution of the linear second-order ordinary differential equation with constant coefficients
x"(t) + ax'(t) + bx(t) = f(t).Then y is a solution of this equation if and only if y(t) = x(t) + z(t) for all t, where z is a solution of the (homogeneous) equationx"(t) + ax'(t) + bx(t) = 0.
- Proof
-
First let y(t) = x(t) + z(t) for all t, where z is a solution of the homogeneous equation, so that z''(t) + az'(t) + bz(t) = 0 for all t. Then
so that y is a solution of the original equation.
y''(t) + ay'(t) + by(t) = [x''(t) + ax'(t) + bx(t)] + [z''(t) + az'(t) + bz(t)] = f(t), Now suppose that y is a solution of the original equation. Define z(t) = y(t) − x(t) for all t. Then
so that z is a solution of the homogeneous equation.z''(t) + az'(t) + bz(t) = [y''(t) + ay'(t) + by(t)] − [x''(t) + ax'(t) + bx(t)] = f(t) − f(t) = 0,
- Procedure for finding general solution of linear second-order ordinary differential equation with constant coefficients
-
The general solution of the differential equation
x"(t) + ax'(t) + bx(t) = f(t)may be found as follows.
- Find the general solution of the associated homogeneous equation x"(t) + ax'(t) + bx(t) = 0.
- Find a single solution of the original equation x"(t) + ax'(t) + bx(t) = f(t).
- Add together the solutions found in steps 1 and 2.
1. Find the general solution of a homogeneous equation
You might guess, based on the solutions we found for first-order equations, that the homogeneous equation has a solution of the form x(t) = Aert. Let's see if it does. If x(t) = Aert then x'(t) = rAert and x"(t) = r2Aert, so that| x"(t) + ax'(t) + bx(t) | = | r2Aert + arAert + bAert |
| = | Aert(r2 + ar + b). |
Suppose that a2 > 4b, so that the characteristic equation has two distinct real roots, say r and s. We have shown that both x(t) = Aert and x(t) = Best, for any values of A and B, are solutions of the equation. Thus also x(t) = Aert + Best is a solution. It can be shown, in fact, that every solution of the equation takes this form.
The cases in which the characteristic equation has a single real root (a2 = 4b) or complex roots (a2 < 4b) require slightly different analyses, with the following conclusions.
- Proposition 8.6.2
-
Consider the homogeneous linear second-order ordinary differential equation with constant coefficients
x"(t) + ax'(t) + bx(t) = 0.The general solution of this equation depends on the character of the roots of the characteristic equation r2 + ar + b = 0 as follows.
- Distinct real roots
- If a2 > 4b, in which case the characteristic equation has distinct real roots, say r and s, the general solution of the equation is
Aert + Best.
- Single real root
- If a2 = 4b, in which case the characteristic equation has a single root, say r, the general solution of the equation is
(A + Bt)ert,where r = −a/2 is the root.
- Complex roots
- If a2 < 4b, in which case the characteristic equation has complex roots, the general solution of the equation is
(Acos(βt) + Bsin(βt))eαt,where α = −a/2 and β = √(b − a2/4). This solution may alternatively be expressed asCeαtcos(βt + ω),where the relationships between the constants C, ω, A, and B are A = C cos ω and B = −C sin ω.
- Source
- For a proof, see Coddington (1961), Theorem 1 on p. 51 and Theorem 5 on p. 58, and Boyce and DiPrima (1969), pp. 106–116.
- Example 8.6.2
-
Consider the differential equation
x"(t) + x'(t) − 2x(t) = 0.The characteristic equation isr2 + r − 2 = 0so the roots are 1 and −2. That is, the roots are real and distinct. Thus the general solution of the differential equation isx(t) = Aet + Be−2t.
- Example 8.6.3
-
Consider the differential equation
x"(t) + 6x'(t) + 9x(t) = 0.The characteristic equation has a single real root, −3. Thus the general solution of the differential equation isx(t) = (A + Bt)e−3t.
- Example 8.6.4
-
Consider the equation
x"(t) + 2x'(t) + 17x(t) = 0.The roots of the characteristic equation are complex. We have a = 2 and b = 17, so α = −1 and β = 4. Thus the general solution of the differential equation is[A cos(4t) + B sin(4t)]e−t.
2. Find a solution of a nonhomogeneous equation
Consider the nonhomogeneous equation| x(t) = |
|
- Example 8.6.5
-
Consider the differential equation
x"(t) + x'(t) − 2x(t) = t2.A linear combination of the function on the right-hand side and its first and second derivatives is C + Dt + Et2. For this function to be a solution,2E + D + 2Et − 2C − 2Dt − 2Et2 = t2 for all t.For this condition to be satisfied (note that the equation must be satisfied for all t), the constant and coefficient of t on the left must be zero and the coefficient of t2 on the left must be 1. That is,The unique solution of these equations is E = −1/2, D = −1/2, and C = −3/4. Thus
2E + D − 2C = 0 2E − 2D = 0 −2E = 1. x(t) = −3/4 − t/2 − t2/2is a solution of the differential equation.
- Example 8.6.6
-
Consider the differential equation
x"(t) − 3x'(t) + 2x(t) = 2et.The characteristic equation is r2 − 3r + 2 = 0, which has roots 1 and 2, so et is a solution of the homogeneous equation. Thus in this case we try x(t) = Atet. We have x'(t) = A(1 + t)et and x"(t) = A(2 + t)et, so for x to be a solution of the differential equation we needA(2 + t)et − 3A(1 + t)et + 2Atet = 2et for all t,or −Aet = 2et for all t, so that A = 2.
Thus a solution of the differential equation is x(t) = −2tet.
3. Add together the solutions found in steps 1 and 2
This step is quite trivial!- Example 8.6.7
-
Consider the equation from a previous example, namely
x"(t) + x'(t) − 2x(t) = t2.We saw above that the general solution of the associated homogeneous equation isx(t) = Aet + Be−2t.and thatx(t) = −3/4 − t/2 − t2/2is a solution of the original equation.
Thus the general solution of the original equation is
x(t) = Aet + Be−2t − 3/4 − t/2 − t2/2.
Second-order initial value problems
A first-order initial value problem consists of a first-order ordinary differential equation x'(t) = F(t, x(t)) and an “initial condition” that specifies the value of x for one value of t. For a second-order equation, requiring an initial condition of that form does not generally determine a unique solution. To determine a unique solution, we generally need to specify both the value of x for some value of t and the rate of change of x at that value of t. Accordingly, we make the following definition.- Definition
-
A second-order initial value problem consists of a second-order ordinary differential equation
x"(t) = F(t, x(t), x'(t))and initial conditionsx(t0) = x0 and x'(t0) = k0where t0, x0, and k0 are numbers.
- Example 8.6.8
-
Consider the second-order initial value problem in which the differential equation is the one in the previous example, namely
x"(t) + x'(t) − 2x(t) = t2,and the initial conditions arex(0) = 0 and x'(0) = 1.From the previous example, the general solution of the equation isx(t) = Aet + Be−2t − 3/4 − t/2 − t2/2.We haveso that for the initial conditions to be satisfied we need
x(0) = A + B − 3/4 x'(0) = A − 2B − 1/2 The unique solution of these equations is A = 1, B = −1/4. Thus the solution of the initial value problem is0 = A + B − 3/4 1 = A − 2B − 1/2. x(t) = et − (1/4)e−2t − 3/4 − t/2 − t2/2.
Equilibrium and stability
The notions of equilibrium and stability for a second-order initial value problem are closely related to the corresponding notions for a first-order initial value problem.- Definition
- If for some initial conditions a second-order initial value problem has a solution that is a constant, the value of the constant is an equilibrium or stationary state of the associated differential equation. If, for all initial conditions, the solution of a second-order initial value problem converges to an equilibrium of the associated differential equation as the variable t increases without bound, then the equilibrium is globally stable.
- Characteristic equation has two real roots
- If the characteristic equation has two real roots, r and s, the general solution of the equation is Aert + Best. This function converges to 0 for all values of A and B, so that the equilibrium is globally stable, if and only if r < 0 and s < 0.
- Characteristic equation has a single real root
- If the characteristic equation has a single real root, r, the general solution of the equation is (A + Bt)ert. This function converges to 0 for all values of A and B, so that the equilibrium is globally stable, if and only if r < 0. (If r < 0 then for any value of k, tkert converges to 0 as t increases without bound.)
- Characteristic equation has complex roots
- If the characteristic equation has complex roots, the general solution of the equation is (Acos(βt) + Bsin(βt))eαt, where α = −a/2, β = √(b − a2/4). This function converges to 0 for all values of A and B, so that the equilibrium is globally stable, if and only if α < 0, or equivalently a > 0. (Remember that cos θ and sin θ lie between +1 and −1 for all values of θ.)
If b = 0, then every number is an equilibrium. By a previous result the general solution of the equation is
Thus an equilibrium of the second-order linear homogeneous equation
Thus we have the following result.
- Proposition 8.6.3
- An equilibrium of the homogeneous linear second-order ordinary differential equation with constant coefficients x"(t) + ax'(t) + bx(t) = 0 is stable if and only if the real parts of both roots of the characteristic equation r2 + ar + b = 0 are negative, or, equivalently, if and only if a > 0 and b > 0.
- Proposition 8.6.4
- For any value of c, an equilibrium of the linear second-order ordinary differential equation with constant coefficients x"(t) + ax'(t) + bx(t) = c with b ≠ 0 is stable if and only if the real parts of both roots of the characteristic equation r2 + ar + b = 0 are negative, or, equivalently, if and only if a > 0 and b > 0.
- Example 8.6.9
-
Consider the following model of an economy with one good. Suppose that the aggregate for the good is
D(t) = a − bp(t) + cπ(t),where p is the price of the good, π is the expected rate of inflation, and a > 0, b > 0, and c > 0 are constants. Suppose that the aggregate supply of the good is fixed at Q*, and that the price adjusts according top'(t) = h(D(t) − Q*) + π(t),where h > 0. Finally, suppose that expectations are adaptive:π'(t) = k(p'(t) − π(t))for some k > 0. Is the equilibrium of this system stable?
One way to answer this question is to reduce the system to a single second-order differential equation by differentiating the equation for p'(t) to obtain p"(t) and then substituting in for π'(t) and π(t). We obtain
p"(t) − h(kc − b)p'(t) + khbp(t) = kh(a − Q*).Given k > 0, h > 0, and b > 0, we have khb > 0, so from the previous proposition the equilibrium is stable if and only if kc < b.In particular, if c = 0 (i.e. expectations are ignored) then the equilibrium is stable. If expectations are taken into account, however, and respond rapidly to changes in the rate of inflation (k is large), then the equilibrium may not be stable.