Mathematical methods for economic theory

Martin J. Osborne
Previous section Previous page Contents Text Exercises Search Next page Next section

5.2 Exercises on local optima

  1. Is x = 1 a local maximum or a local minimum of the function f(x) = −x3 + 3x − 2, or neither?

    Solution

    f'(x) = −3x2 + 3 and f"(x) = −6x, so f'(1) = 0 and f"(1) = −6 < 0. Thus x = 1 is a local maximizer.
  2. Find all the local maxima and minima (if any) of the following functions.
    1. f(x, y) = −x2 + xy − y2 + 2x + y
    2. f(x, y) = e2x − 2x + 2y2 + 3

    Solution

    1. f'1(x, y) = −2x + y + 2 and f'2(x, y) = x − 2y + 1. So the first-order conditions have a unique solution, (x, y) = (5/3, 4/3). We have f"11(x, y) = −2, f"22(x, y) = −2, and f"12(x, y) = 1, so f"11(5/3, 4/3)f"22(5/3, 4/3) − (f"12(5/3, 4/3))2 = 3 > 0. Hence the Hessian of f is negative definite at (5/3, 4/3), so that (x, y) = (5/3, 4/3) is a local maximizer.

    2. f'1(x, y) = 2e2x − 2, f'2(x, y) = 4y. So the first-order conditions have a unique solution, (x, y) = (0, 0). We have f"11(x, y) = 4e2x, f"22(x, y) = 4, and f"12(x, y) = 0, so f"11(0, 0)f"22(0, 0) − (f"12(0, 0))2 = 16e2x > 0. Hence the Hessian of f is positive definite at (0, 0), so that (x, y) = (0, 0) is a local minimizer.
  3. Find all the local maxima and minima and all the global maxima and minima, if any, of the following functions. For any extreme point that you find, give both the maximizer or minimizer (value of x) and the maximum or minimum (value of f(x)).
    1. f(x) = x2 + 3 on [−1, 1]
    2. f(x) = x3 − 3x + 5 on [−3, 3]
    3. f(x) = x + 1/x on [1/2, 2]
    4. f(x) = (x − 2)6 on [0, 4].

    Solution

    1. We have f'(x) = 2x, so the function has a single stationary point, x = 0. We have also f"(x) = 2 > 0, so x = 0 is a local minimizer. We have also f(−1) = 4 and f(1) = 4, so that x = 0 is the only global minimizer (value 3), and x = −1 and x = 1 are both global maximizers (value 4).
    2. We have f'(x) = 3x2 − 3, so the function has two stationary points, x = 1 and x = −1. We have f"(x) = 6x, so that f"(1) > 0 and f"(−1) < 0. Thus x = 1 is a local minimizer (minimum value 3) and x = −1 is a local maximizer (maximum value 7). We have also f(−3) = −13 and f(3) = 23, so x = −3 is the only global minimizer (value −13) and x = 3 is the only global maximizer (value 23).
    3. We have f'(x) = 1 − 1/x2, so the function has a single stationary point in the interval [1/2, 2], namely x = 1. We have f"(x) = 2/x3, so x = 1 is a local minimizer (value 2). We have also f(1/2) = 5/2 and f(2) = 5/2, so x = 1 is the only global minimizer (value 2) and x = 1/2 and x = 2 are both global maximizers (value 5/2).
    4. We have f'(x) = 6(x − 2)5, so the function has a single stationary point, x = 2. We have f"(x) = 30(x − 2)4, so that f"(2) = 0. Thus this information is not enough to tell us whether x = 2 is a local maximizer or minimizer, or neither. We have also f(0) = 64 and f(4) = 64, so x = 2 is the only global minimizer (value 0), and x = 0 and x = 4 are both global maximizers (value 64). We conclude that x = 2 is the only local minimizer, and x = 0 and x = 4 are both local maximizers.
  4. Find all the local maxima (if any) of the following functions. For each local maximum that you find, determine, if possible, whether it is a global maximum.
    1. f(x, y) = (1/3)x3 + 2xy − 2y2 − 6x.
    2. f(x, y) = 3xy − x3 − y3.

    Solution

    1. The first-order conditions are
      x2 + 2y − 6  = 0
      2x − 4y  = 0.
      From the second equation we have x = 2y, so from the first equation we have
      4y2 + 2y − 6 = 0,
      or
      2y2 + y − 3 = 0,
      or
      (2y + 3)(y − 1) = 0.
      Thus y = 1 or y = −(3/2). Hence the equations have two solutions: (2, 1) and (−3, −3/2).

      The Hessian of the function is

      left parenthesis 2x 2 right parenthesis
      2 −4
      		.
      For x = 2 this matrix is indefinite; f"x(2, 1) > 0 and f"y(2, 1) < 0, so (2, 1) is a saddle point. For x = −3 the matrix is negative definite, so that (−3, −3/2) is a local maximizer.

      The point (−3, −3/2) is not a global maximizer, because for y = 0 and x arbitrarily large, the value of the function is arbitrarily large.

    2. The first-order conditions are
      3y − 3x2  = 0
      3x − 3y2  = 0.
      These equations have two solutions, (0, 0) and (1, 1).

      The Hessian of the function is

      left parenthesis −6x 3 right parenthesis
      3 −6y
      At (1,1) this Hessian is negative definite, while at (0,0) it is indefinite.

      Thus (1,1) is a local maximizer. It is not a global maximizer, because f(1, 1) = 1, while f(−1, −1) = 5 (for example).

  5. If (x*, y*) minimizes f(x, y) then x* minimizes f(x, y*) and y* minimizes f(x*, y). But we know that the fact that x* minimizes f(x, y*) and y* minimizes f(x*, y) is not sufficient for (x*, y*) to minimize f(x, y). If (x*, y*) minimizes f(x, y) along all lines through (x*, y*), not only the lines parallel to the axes, does (x*, y*) necessarily minimize f? Use the function f defined by f(x, y) = (y − x2)(y − 2x2) for all (x, y) to study this question.
    1. Draw a figure showing the regions of the (x, y) plane at which this function has positive values and the regions at which it has negative values.
    2. Fix a number a and restrict attention to values of x and y for which x = ay. That is, for each number a, consider the function ga(y) = f(ay, y). Show that for every value of a the point y = 0 is a local minimum of ga(y).
    3. Is the point (x, y) = (0,0) a local minimum of f?

    Solution

    1. In the figure below, the function is positive in the red region (i.e. when x > y2 and x > 2y2, or x < y2 and y < 2y2) and negative in the green region.

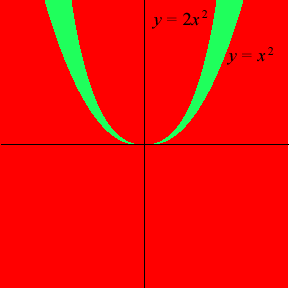
    2. We have ga(y) = f(ay, y) = (y − a2y2)(y − 2a2y2) = y2 − 3a2y3 + 2a4y4. The derivative is 2y − 9a2y2 + 8a4y3, which is zero when y = 0. The second derivative is 2 − 18a2y + 24a4y2, which is positive at y = 0, so for any value of a the function has local minimum at 0.
    3. No: look at the diagram for part (a). Every disk centered at (0, 0), not matter how small, contains points at which the function is negative (points between the two parabolas).
  6. Find all the local maxima and minima and all the global maxima and minima, if any, of the following functions. For any extreme point that you find, give both the maximizer or minimizer (value of x) and the maximum or minimum (value of f(x)).
    1. f(x) = 3x3 − 5x2 + x on the interval [0, 1]
    2. f(x) = 3x3 − 5x2 + x on the interval [0, 2]
    3. f(x) = (x − 4)2 + 5 on the interval [−5, 5]

    Solution

    1. First find the stationary points: these are the solutions of f'(x) = 0, or 9x2 − 10x + 1 = 0, or (9x − 1)(x − 1) = 0. Thus the stationary points are x = 1/9 and x = 1. The values of the function at these points are f(1/9) = 3(1/9)3 − 5(1/9)2 + 1/9 = (1/243)[1 − 15 + 27] = 13/243 and f(1) = −1.

      Now find the values of the function at the endpoints of the interval: f(0) = 0 and f(1) = −1.

      Thus the (global) maximizer of the function on the interval [0, 1] is x = 1/9 and the (global) minimizer is x = 1. (There are no other local maximizers or minimizers.)

    2. As in the previous part, the stationary points are x = 1/9 and x = 1, with f(1/9) = 13/243 and f(1) = −1.

      The values of the function at the endpoints of the interval are f(0) = 0 and f(2) = 6.

      Thus the (global) maximizer of the function on the interval [0, 2] is x = 2 and the (global) minimizer is x = 1.

      The only other stationary point is x = 1/9. We have f"(x) = 18x − 10, so that f"(1/9) < 0. Thus x = 1/9 is a local maximizer.

    3. We have f'(x) = 2(x − 4) and hence f"(x) = 2 for all values of x. Thus the function f is convex. Hence any stationary point is a global minimizer.

      There is a single stationary point, x = 4. Thus the function has a single global minimizer, x = 4.

      We have f(−5) = 86 and f(5) = 6, so the global maximizer is x = −5.

  7. Consider the function f(x, y) = (x − 2)4 + (y − 3)4.
    1. Show that this function has a minimum at (x, y) = (2, 3) (without using any calculus).
    2. Find all the solutions of the first-order conditions.
    3. Is the Hessian of f positive definite at any solution of the first-order conditions?

    Solution

    1. f(2, 3) = 0 ≤ (x − 2)4 + (y − 3)4 for any x and y, because z4 ≥ 0 for all z.

    2. f1'(x, y) = 4(x − 2)3, f2'(x, y) = 4(y − 3)3. So the only solution of first-order conditions is (x, y) = (2, 3).

    3. f"11(x, y) = 12(x − 2)2, f"22(x, y) = 12(y − 3)2, and f"12(x, y) = 0, so that we have f"11(2, 3)·f"22(2, 3) − (f"12(2, 3))2 = 0. Thus the Hessian is not positive definite at any solution of the first-order conditions. (Hence we cannot conclude from the second-order conditions that (2, 3) is a minimizer of the function, though we know that it is.)
  8. Find all the local maximizers and minimizers of the following functions.
    1. f(x1, x2, x3) = x2
      1       + 3x2
      2       − 3x1x2 + 4x2x3 + 6x2
      3      .
    2. f(x1, x2, x3) = 29 − (x2
      1       + x2
      2       + x2
      3      ).
    3. f(x1, x2, x3) = x1x3 + x2
      1       − x2 + x2x3 + x2
      2       + 3x2
      3      .

    Solution

    1. First-order conditions:
      f'1(x1, x2, x3) = 2x1 − 3x2  = 0
      f'2(x1, x2, x3) = −3x1 + 6x2 + 4x3  = 0
      f'3(x1, x2, x3) = 4x2 + 12x3  = 0
      These conditions have a unique solution, (x1, x2, x3) = (0, 0, 0). The Hessian matrix is
      left parenthesis 2 −3 0 right parenthesis
      −3 6 4
      0 4 12
      The leading principal minors are 2 > 0, 3 > 0, and (2)(72−16)−(−3)(−36) = 4 > 0, so that (x1, x2, x3) = (0,0,0) is a local minimizer. (The function is convex, so this minimum is in fact a global minimizer.)
    2. First-order conditions: f'i(x1, x2, x3) = −2xi = 0 for i = 1, 2, 3. There is a unique solution, (x1, x2, x3) = (0,0,0). The Hessian matrix is
      left parenthesis −2 0 0 right parenthesis
      0 −2 0
      0 0 −2
      The leading principal minors are −2 < 0, 4 > 0, and (−2)(4) = −8 < 0, so that (x1, x2, x3) = (0,0,0) is a local maximizer.

    3. First-order conditions:
      f'1(x1, x2, x3) = 2x1 + x3  = 0
      f'2(x1, x2, x3) = 2x2 + x3 − 1  = 0
      f'3(x1, x2, x3) = x1 + x2 + 6x3  = 0
      These conditions have a unique solution, (x1, x2, x3) = (1/20, 11/20, −2/20). The Hessian matrix is
      left parenthesis 2 0 1 right parenthesis
      0 2 1
      1 1 6
      The leading principal minors are 2 > 0, 4 > 0, and (2)(11) + (1)(−2) = 20 > 0, so that (x1, x2, x3) = (1/20, 11/20, −2/20) is a local minimizer.