3.3 Concave and convex functions of many variables
Convex sets
To extend the notions of concavity and convexity to functions of many variables we first define the notion of a convex set.
- Definition
-
A set S of n-vectors is convex if
(1−λ)x + λx' ∈ S whenever x ∈ S, x' ∈ S, and λ ∈ [0,1].
For n = 1, the definition coincides with the definition of an interval: a set of numbers is convex if and only if it is an interval.
For n = 2, two examples are given in the following figures. The set in the first figure is convex, because every line segment joining a pair of points in the set lies entirely in the set. The set in the second figure is not convex, because the line segment joining the points x and x' does not lie entirely in the set.
The following property of convex sets (which you are asked to prove in an exercise) is sometimes useful.
- Proposition 3.3.1
- The intersection of convex sets is convex.
Concave and convex functions
Let f be a function of many variables, defined on a convex set S. We say that f is concave if the line segment joining any two points on the graph of f is never above the graph; f is convex if the line segment joining any two points on the graph is never below the graph. (That is, the definitions are the same as the definitions for functions of a single variable.)More precisely, we can make the following definition (which is again essentially the same as the corresponding definition for a function of a single variable). Note that only functions defined on convex sets are covered by the definition.
- Definition
-
Let f be a function of many variables defined on a convex set S. Then f is
- concave if for all x ∈ S, all x' ∈ S, and all λ ∈ (0,1) we have
f((1−λ)x + λx') ≥ (1−λ)f(x) + λf(x') - convex if for all x ∈ S, all x' ∈ S, and all λ ∈ (0,1) we have
f((1−λ)x + λx') ≤ (1−λ)f(x) + λf(x').
- concave if for all x ∈ S, all x' ∈ S, and all λ ∈ (0,1) we have
- Definition
-
Let f be a function of many variables defined on a convex set S. Then f is
- strictly concave if for all x ∈ S, all x' ∈ S with x' ≠ x, and all λ ∈ (0,1) we have
f((1−λ)x + λx') > (1−λ)f(x) + λf(x') - strictly convex if for all x ∈ S, all x' ∈ S with x' ≠ x, and all λ ∈ (0,1) we have
f((1−λ)x + λx') < (1−λ)f(x) + λf(x').
- strictly concave if for all x ∈ S, all x' ∈ S with x' ≠ x, and all λ ∈ (0,1) we have
- Example 3.3.1
-
Let f be a linear function, defined by f(x) = a1x1 + ... + anxn = a·x on a convex set, where ai is a constant for each i. Then
f is both concave and convex:
f((1 − λ)x + λx') = a·[(1−λ)x + λx'] for all x, x', and λ ∈ [0, 1] = (1−λ)a·x + λa·x' for all x, x', and λ ∈ [0, 1] = (1−λ)f(x) + λf(x') for all x, x', and λ ∈ [0, 1].
- Example 3.3.2
-
Suppose the function g of a single variable is concave on [a,b], and the function f of two variables is defined by f(x,y) = g(x) on [a, b] × [c, d]. Is f concave?
First note that the domain of f is a convex set, so the definition of concavity can apply.
The functions g and f are illustrated in the following figures. (The axes for g are shown in perspective, like those for f, to make the relation between the two figures clear. If we were plotting only g, we would view it straight on, so that the x-axis would be horizontal. Note that every cross-section of the graph of f parallel to the x-axis is the graph of the function g.)
From the graph of f (the roof of a horizontal tunnel), you can see that it is concave. The following argument is precise.
so f is concave.f((1−λ)(x, y) + λ(x', y')) = f((1−λ)x + λx', (1−λ)y + λy') = g((1−λ)x + λx') ≥ (1−λ)g(x) + λg(x') = (1−λ)f(x, y) + λf(x', y')
- Example 3.3.3
-
Let f and g be defined as in the previous example. Assume now that g is strictly concave. Is f strictly concave?
The strict concavity of f implies that
for all x ≠ x'. But to show that f is strictly concave we need to show that the inequality is strict whenever (x, y) ≠ (x', y')—in particular, for cases in which x = x' and y ≠ y'. In such a case, we havef((1−λ)(x, y) + λ(x', y')) > (1−λ)f(x, y) + λf(x', y') Thus f is not strictly concave. You can see the lack of strict concavity in the figure (in the previous example): if you take two (x, y) pairs with the same value of x, the line joining them lies everywhere on the surface of the function, never below it.f((1−λ)(x, y) + λ(x', y')) = f(x, (1−λ)y + λy') = g(x) = (1−λ)f(x, y) + λf(x, y').
Characterizations of concave and convex functions
Having seen many examples of concave functions, you should find it plausible that a function is concave if and only if the set of points under its graph—the set shaded pink in the following figure—is convex. The result is stated precisely in the following proposition.
- Proposition 3.3.2
- A function f of many variables defined on a convex set S is
- Proof
-
Let L = {(x, y): x ∈ S and y ≤ f(x)}.
First suppose f is concave and let (x, y) ∈ L and (x', y') ∈ L. Then x ∈ S, x' ∈ S, y ≤ f(x) and y' ≤ f(x'). The last two inequalities imply that
Now, because S is convex, (1 − λ)x + λx' ∈ S, so that (1 − λ)x + λx' is in the domain of f, and because f is concave,(1 − λ)y + λy' ≤ (1 − λ)f(x) + λf(x') for any λ ∈ [0, 1]. (1 − λ)f(x) + λf(x') ≤ f((1 − λ)x + λx').Thus(1 − λ)y + λy' ≤ f((1 − λ)x + λx'),and hence ((1 − λ)x + λx', (1 − λ)y + λy') = (1 − λ)(x, y) + λ(x', y') ∈ L, establishing that L is convex.Conversely, suppose L is convex. Let x ∈ S and x' ∈ S. Then (x, f(x)) ∈ L and (x', f(x')) ∈ L, so by the convexity of L, (1 − λ)(x, f(x)) + λ(x', f(x')) = ((1 − λ)x + λx', (1 − λ)f(x) + λf(x')) ∈ L for any λ ∈ [0, 1]. Thus (1 − λ)f(x) + λf(x') ≤ f((1 − λ)x + λx'), establishing that f is concave.
The argument for a convex function is symmetric.
- Proposition 3.3.3 (Jensen's inequality)
-
A function f of many variables defined on a convex set S is concave if and only if for all n ≥ 2
for all x1 ∈ S, ..., xn ∈ S and all λ1 ≥ 0, ..., λn ≥ 0 with ∑n
f(λ1x1 + ... + λnxn) ≥ λ1f(x1) + ... + λnf(xn)
i=1λi = 1.The function f of many variables defined on the convex set S is convex if and only if for all n ≥ 2
for all x1 ∈ S, ..., xn ∈ S and all λ1 ≥ 0, ..., λn ≥ 0 with ∑nf(λ1x1 + ... + λnxn) ≤ λ1f(x1) + ... + λnf(xn)
i=1λi = 1.
- Proof
-
Here is the proof for concavity; the proof for convexity is analogous.
If the inequality is satisfied for all n, it is satisfied in particular for n = 2, so that f is concave directly from the definition of a concave function.
Now suppose that f is concave. Then the definition of a concave function implies directly that the inequality is satisfied for n = 2. To show that it is satisfied for all n ≥ 3 I argue by induction. Let m ≥ 2 and suppose that the inequality is satisfied for all n ≤ m. I show that it is satisfied for n = m + 1. Take any x1 ∈ S, ..., xm+1 ∈ S and λ1 ≥ 0, ..., λm+1 ≥ 0 with ∑m+1
i=1λi = 1. If λ1 = 1 then λ2 = ... = λm+1 = 0, so that the inequality is trivially satisfied. If λ1 < 1 thenby taking x = x1, x' = ∑m+1f(∑m+1
i=1λixi)= f(λ1x1 + (1 − λ1)∑m+1
i=2(λi/(1−λ1))xi)≥ λ1f(x1) + (1 − λ1)f(∑m+1
i=2(λi/(1−λ1))xi)
i=2(λi/(1−λ1))xi, and λ = 1 − λ1 in the definition of a concave function. Now, because the inequality is satisfied for n = m we haveso thatf(∑m+1
i=2(λi/(1−λ1))xi)≥ ∑m+1
i=2(λi/(1−λ1))f(xi),completing the argument.f(∑m+1
i=1λixi)≥ λ1f(x1) + (1 − λ1)∑m+1
i=2(λi/(1−λ1))f(xi)= ∑m+1
i=1λif(xi),
Differentiable concave and convex functions
A previous result shows that the graph of a concave function of a single variable lies everywhere on or below all of its tangents. The generalization of this result to concave functions of many variables says that the graph of such a function lies everywhere on or below all of its tangent planes. As for a function of a single variable, a symmetric result holds for convex functions. Like the result for functions of a single variable, it is used to show that stationary points are global maximizers of concave functions and global minimizers of convex functions.- Proposition 3.3.4
-
The differentiable function f of n variables defined on an open convex set S is concave on S if and only if
and is convex on S if and only if
f(x) − f(x*) ≤ ∑n
i=1f'i(x*)·(xi − x*i) for all x ∈ S and x* ∈ Sf(x) − f(x*) ≥ ∑n
i=1f'i(x*)·(xi − x*i) for all x ∈ S and x* ∈ S.
- Source
- One proof follows the lines of the proof of the analogous result for a function of a single variable. For details, see Sydsæter and Hammond (1995), Theorem 17.7 (p. 629). (Note that by this result their assumption that the function has continuous partial derivatives is equivalent to the assumption that the function is continuously differentiable, and by Corollary 25.5.1 (p. 246) in Rockafellar (1970), a differentiable convex function, and hence a differentiable concave function, is continuously differentiable.) Simon and Blume (1994), Theorem 21.3 (p. 511), give a different proof.
Twice-differentiable concave and convex functions
A twice-differentiable function of a single variable is concave if and only if its second derivative is nonpositive everywhere.To determine whether a twice-differentiable function of many variables is concave or convex, we need to examine all its second partial derivatives. We call the matrix of all the second partial derivatives the Hessian of the function.
- Definition
-
Let f be a twice-differentiable function of n variables. The Hessian of f at x is
H(x) = 
f"11(x) f"12(x) ... f"1n(x) 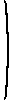
f"21(x) f"22(x) ... f"2n(x) ... ... ... ... f"n1(x) f"n2(x) ... f"nn(x) .
We can determine the concavity/convexity of a function by determining whether the Hessian is negative or positive semidefinite, as follows.
- Proposition 3.3.5
-
Let f be a twice-differentiable function of many variables defined on an open convex set S and denote the Hessian of f at the point x by
H(x). Then
- f is concave if and only if H(x) is negative semidefinite for all x ∈ S
- if H(x) is negative definite for all x ∈ S then f is strictly concave
- f is convex if and only if H(x) is positive semidefinite for all x ∈ S
- if H(x) is positive definite for all x ∈ S then f is strictly convex.
- Source
- For a proof, see Sydsæter and Hammond (1995), Theorems 17.13 (p. 640) and 17.14 (p. 641).
The result implies the following procedure.
- Procedure for checking the concavity/convexity and strict concavity/convexity of a function of many variables
-
- Hessian negative definite for all x ⇒ function is strictly concave; Hessian positive definite for all x ⇒ function is strictly convex.
- Hessian not negative semidefinite for all x ⇒ function is not concave, and hence not strictly concave; Hessian not positive semidefinite for all x ⇒ function is not convex, and hence not strictly convex.
- Hessian negative semidefinite for all x but not negative definite for all x ⇒ function is concave and may or may not be strictly concave; you need to use other methods (for example, the basic definition of concavity) to determine whether it is strictly concave. Similarly, Hessian positive semidefinite for all x but not positive definite for all x ⇒ function is convex and may or may not be strictly convex.
- Example 3.3.4
-
Consider the function f(x, y) = 2x − y − x2 + 2xy − y2 defined on the set of all pairs of numbers. Its Hessian is
which is negative semidefinite, but not negative definite (its determinant is zero). (For this function, the Hessian does not depend on (x, y); in general it does.) Thus f is concave; the analysis does not tell us whether it is strictly concave.

−2 2 
2 −2
- Example 3.3.5
-
Consider the function f(x1, x2, x3) = x2
1 + 2x2
2 + 3x2
3 + 2x1x2 + 2x1x3 defined on the set of all triples of numbers. Its first partials areSo its Hessian isf'1(x1, x2, x3) = 2x1 + 2x2 + 2x3 f'2(x1, x2, x3) = 4x2 + 2x1 f'3(x1, x2, x3) = 6x3 + 2x1. The leading principal minors of the Hessian are 2 > 0, 4 > 0, and 8 > 0. So the Hessian is positive definite, and f is strictly convex.
f"11 f"12 f"13 
f"21 f"22 f"23 f"31 f"32 f"33 = 
2 2 2 
2 4 0 2 0 6 .
- Example 3.3.6
-
Consider the Cobb-Douglas function, defined by f(K, L) = AKaLb on the set of pairs (K, L) with K ≥ 0 and L ≥ 0. Assume that A > 0. The Hessian of this function is
Thus for f to be concave on the set of pairs (K, L) with K ≥ 0 and L ≥ 0 we need a(a−1)AKa−2Lb ≤ 0, b(b−1)AKaLb−2 ≤ 0, and abA2K2a−2L2b−2(1 − (a + b)) ≥ 0 for all K ≥ 0 and L ≥ 0. Thus f is concave on this set if and only if a ≥ 0, b ≥ 0, and a + b ≤ 1 (so that a ≤ 1 and b ≤ 1). Similarly, it is strictly concave on the set of pairs (K, L) with K > 0 and L > 0 if a > 0, b > 0, and a + b < 1 (so that a < 1 and b < 1). (In fact, under these conditions it is strictly concave on the set of pairs (K, L) with K ≥ 0 and L ≥ 0, but this conclusion does not follow from the signs of the minors of the Hessian.)

a(a−1)AKa−2Lb abAKa−1Lb−1 
abAKa−1Lb−1 b(b−1)AKaLb−2 .
Two properties of concave and convex functions
The following result says that any weighted sum of concave functions with nonnegative weights is concave; the proof is an exercise.- Proposition 3.3.6
- Let f and g be functions of many variables defined on a convex set S.
- Example 3.3.7
-
A firm produces the output f(x) from the vector x of inputs, which costs it c(x). The function f is concave and the function c is convex. The firm sells its output at a fixed price p > 0. Its profit when it uses the input vector x is
π(x) = pf(x) − c(x).That is, π is the sum of two functions, pf and −c. The function −c is concave because c is convex, so by the proposition π is concave.
- Proposition 3.3.7
- Let U be a function of many variables defined on a convex set S and let g be a function of a single variable defined on a set that contains the range of U.